特性インピーダンスの測定

ボードのパターンの特性インピーダンスは、通常、TRD (Time Domain Reflectmety) 法で測定します。

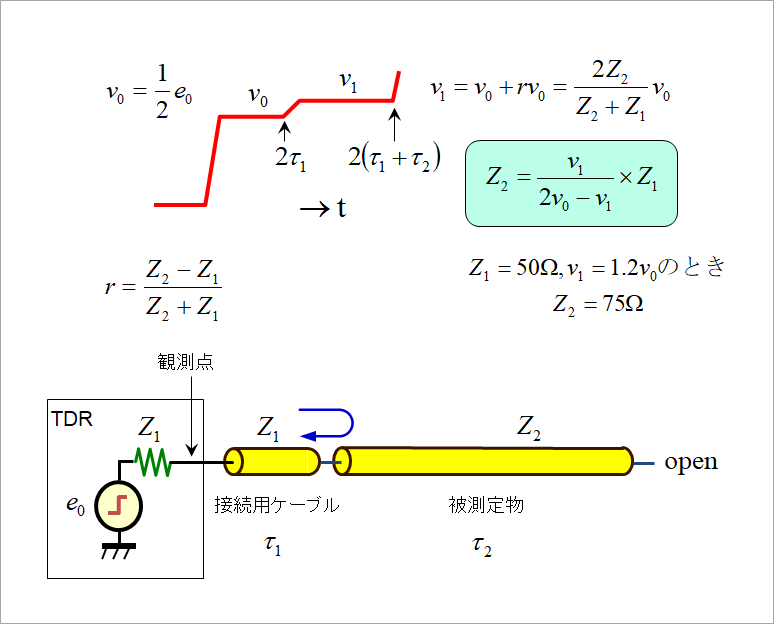
図1 はその測定の等価回路です。TDR 本体からは、立ち上がり時間が、数10ps 以下の極めて速いパルス波形か送出されます。線路の特性インピーダンスの測定だけなら、これほど速い立ち上がりは必要ありませんが、微小なキャパシタやインダクタの影響を調べたり、数ミリの線路の特性インピーダンスの不連続を調べる場合には、このように速い立ち上がりのパルスを必要とします。

TDR の測定原理

TDR の出力インピーダンスを Z1（通常は 50Ω）とし、TDR と被測定物（DUT）とは、特性インピーダンスが Z1 (50Ω) のケーブルで接続されます。このケーブルは、通常、損失が無視できる理想のケーブルとみなせるので、TDR の出力インピーダンスとの接続点においては反射が発生しません。ケーブル（特性インピーダンス Z1）と DUT（特性インピーダンス Z2）との接続点における反射係数は、r=(Z2-Z1)/(Z2+Z1) です。（豆知識「反射係数」を参照ください。）

以下、式が見づらいので、図2 に式だけ抜粋して示します。本文と見比べながらご覧ください。

ケーブルと DUT との接続点における電圧 v1 は、入射波を v0 とすると、
　v1=v0+rv0=2Z2/(Z2+Z1)v0
となり、この式から Z2 を求めると、
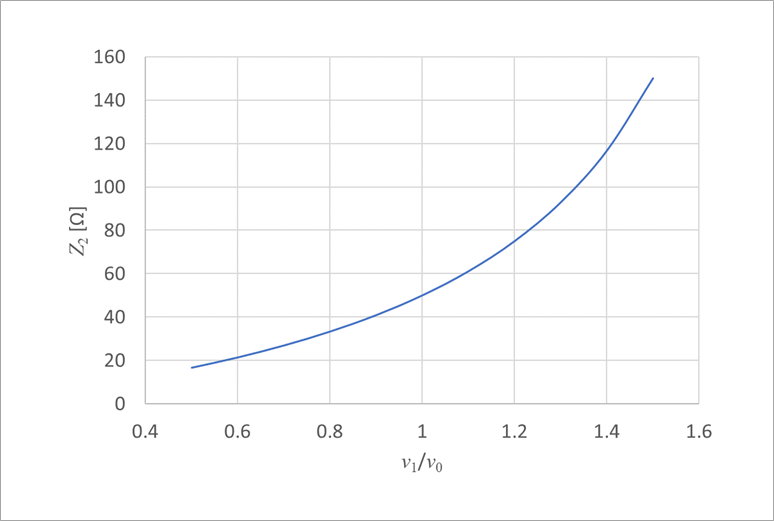
　Z2=v1/(2v0-v1)×Z1=v1/v0/(2-v1/v0)×Z1
となります。

図3 に、v1/v0 に対する DUT の特性インピーダンス Z2 を、Z1=50と して示します。すなわち、最初の立ち上がりの振幅で特性インピーダンスを読み取ることができることを示します。TDR は実際には、この演算を施した目盛りにより Z2 を直読できるように設定されています。

特性インピーダンスの式と線路損失

線路の特性インピーダンス Z0 は、線路のインダクタ L (H/m) とキャパシタ C (F/m) によって、Z0=√(L/C) で表されます。（「分布定数回路～何が分布しているのか？」を参照ください。）

実際の線路には、抵抗損と誘電損による損失が存在します。（「線路損失と波形」を参照ください。）

これらの線路損失は、周波数の関数なので、PSPICE のような簡単な SPICE では解析が困難です。一般的には、HyperLynx や HSPICE の W エレメントなどを用います。筆者は、周波数軸で解いて、FFT で時間軸に変換して波形を求めています。線路損失を考慮した特性インピーダンスは、
　Z0=√{(R+jωL)/(G+jωC)}
で表されます。例えば、1GHz における差動インピーダンス 85Ω の線路の線路定数の一例は、
　L-Lm=315nH/m → ω(L-Lm)=1979
　C-Cm=150pF/m → ω(C-Cm)=0.942
　R=58Ω
　tanδ=0.02 → G=0.02
です。

R≪ωL、G≪ωC であることを考慮して、Z0 の式を書き換えます。
　Z0=√(L/C)×√{(1+R/jωL)/(1+G/jωC)}
　　　≒√(L/C)×{1+(R/L-G/C)/(j2ω)}
時間応答を求めるために、ラプラス変換のsを用いて、上式の jω→s とおくと、
　Z0≒√(L/C)×{1+(R/L-G/C)/2s}=Z00×(1+a/s)
となります。以下の式の変形を、図4 に示します。ここに、
　Z00=√(L/C)
　a=(R/L-G/C)/2
とします。

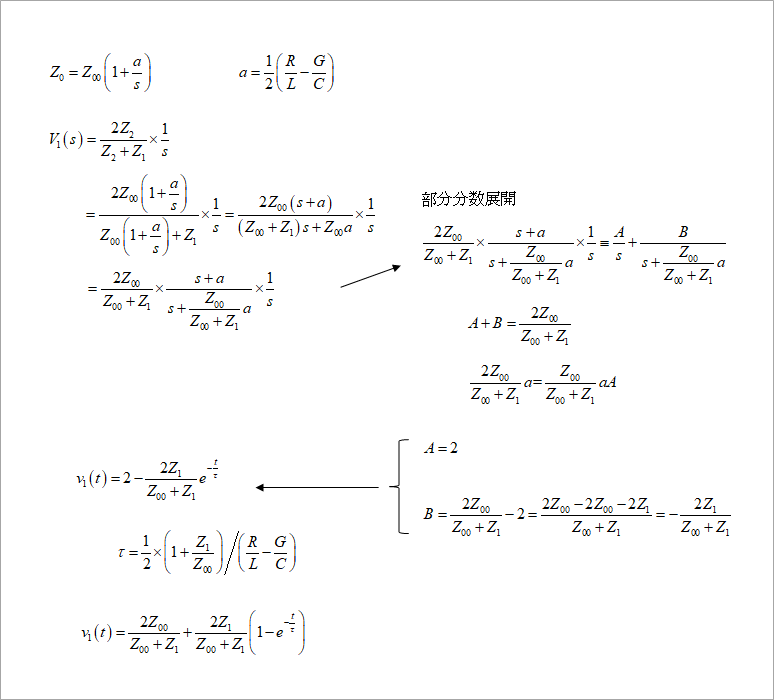
ラプラス変換による時間応答

この Z0 を、v1 の式の Z2 に代入して、ステップ応答を求めます。ステップ波形のラプラス変換は、1/s なので、
　V1(s)=2Z2/(Z2+Z1)/s
この後の変形は煩雑なので、図4 にまとめました。上式を、部分分数展開して、ラプラス逆変換すると、
　v1は、2-2Z1/(Z00+Z1)exp(-t/τ)
となり、t=∞ で 2 に収束します。上式を書き換えると、
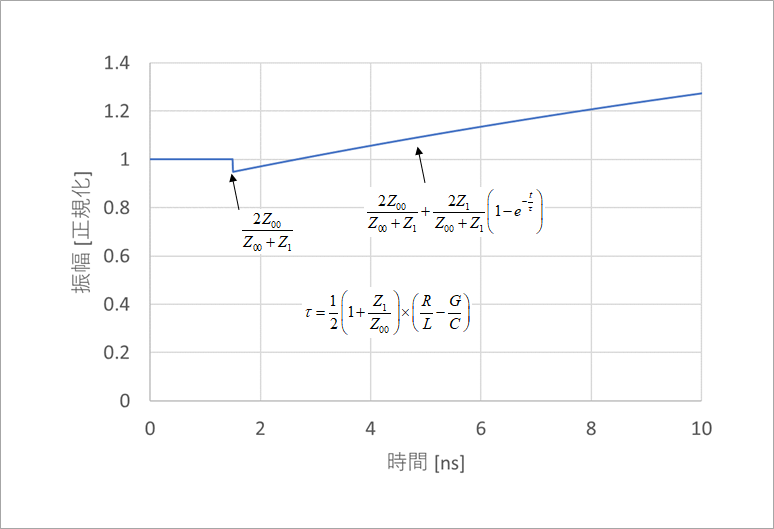
　v1=2Z00/(Z00+Z1)+2Z1/(Z00+Z1){1-exp(-t/τ)}
となり、図5 にその計算例を示します。上の例で、G=0 としました。τ は、23ns 程度になります。

TDR の波形

実際には、かなり短い時間で遠端からの反射が戻り、DUT の線長によって、この指数波形が中断されることになるので、「基板の特性インピーダンスコントロール」の 図7 のような TDR の波形となります。

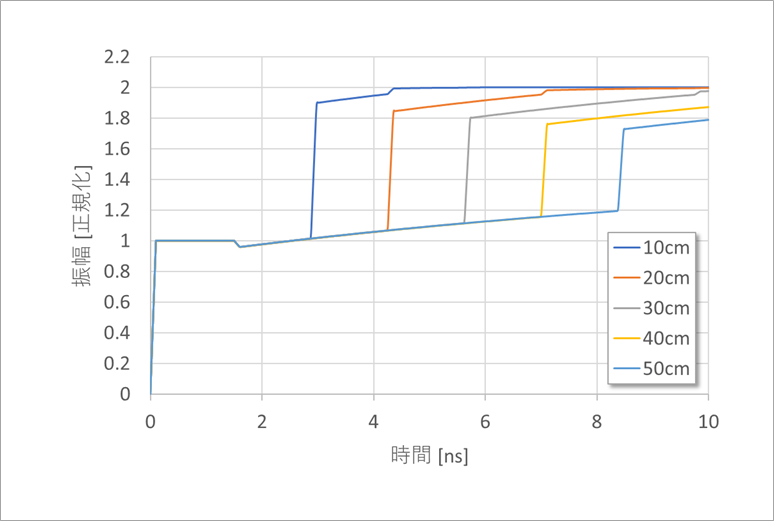
筆者は、MicroCap という PSPICE を用いていますが、その解析波形した結果を、図6 に示します。この SPICE は、誘電損が扱えないので、抵抗損のみ与えています。また、この抵抗損の周波数依存は反映していません。

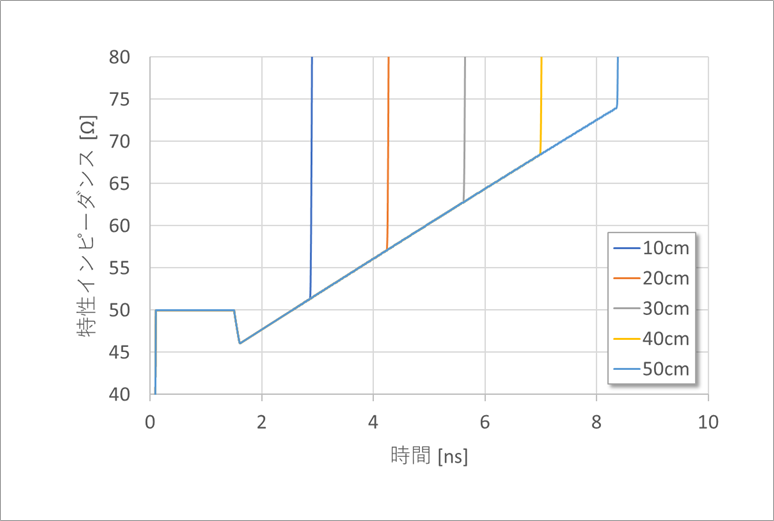
図7 は、v1 の値を特性インピーダンスに変換して示したものです。「基板の特性インピーダンスコントロール」の 図7 に近い特性が得られました。実際には、抵抗の周波数特性（表皮効果）や誘電損を反映させる必要がありますが、TDR の波形が傾きを有することは理解できると思います。

なお、抵抗を 1GHz のときの表皮抵抗としたので、波形の傾きが誇張されています。実際の特性を求めるには、上に述べたように、R、G の周波数依存が解析できるソフトや FFT による計算が必要です。

参考文献
碓井有三 : ボード設計者のための分布定数回路のすべて(第3版) 自費出版 (http://home.wondernet.ne.jp/~usuiy/), pp. 171-180, 2016