分布している「定数」とは、キャパシタ（Capacitor）とインダクタ（Inductor）などの回路素子を指します。（脚注1）

配線とグラウンドとの間にキャパシタンス（または静電容量）が存在するのは何となく理解できると思います。プリント配線板の場合、1 cm 当たり、およそ 1 pF（ピコフラッド）の容量があります。インダクタンスは、1 cm 当たり 3 ~ 5 nH（ナノヘンリー）程度です。

この 1 cm 当たりというのは、これらの回路素子が「分布して」存在するということを意味します。1 cm 当たり 1 pF ということは、1 m だと 100 pF に相当します。キャパシタもインダクタもどちらも分布して存在します。これを等価回路で書き表すと、図1のようになります。この一つ一つの素子が先に述べたように分布して存在しているわけです。

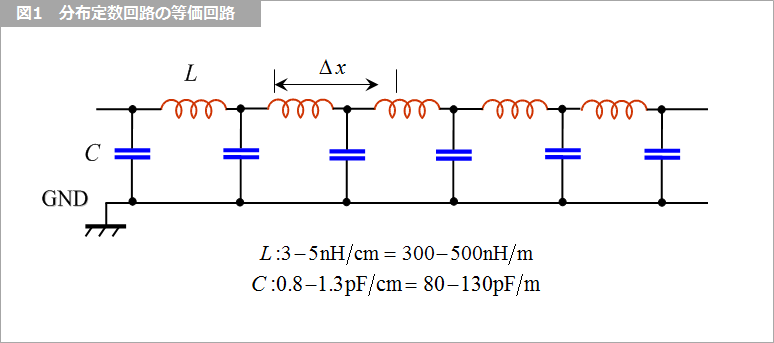
この等価回路の 1 区間 Δx はどのくらいの長さでしょうか。何ミリとか何センチとかの具体的な長さはありません。理論的には無限に短い区間です。微分と同じ考え方です。とはいっても、SPICE（スパイス）のような回路解析ソフトで等価回路を作るとしたら、具体的な長さが必要になります。このようなときにどのくらいの長さを選ぶかについてはまた別の機会に述べることとしますが、高速信号の場合はミリメートルのオーダーで、あまり速くない信号の場合は 1 cm 程度に選ぶこともあります。短く（細かく）選ぶと精度は上がりますが、解析時間が長くなるので、ある程度の妥協が必要となります。

キャパシタとインダクタが分布しているので、この両者でエネルギーをバトンタッチして信号を伝えます。この回路には抵抗分が含まれていません。実際には、小さな抵抗成分があります。ごく普通のプリント配線板のパターンには、1 メートル当たり 4 Ω 程度の抵抗があります。普通の信号伝送では、この抵抗分は無視できるので、損失を考えません。バケツに水を入れて、次々にリレーしていくようなものです。バケツに穴が開いてなくて、リレーの際にこぼさなければ、理論的には何メートルでも水の量は減らないのと同じことです。バケツに穴が開いていたり、リレーの際に水をこぼすような信号伝送路を損失線路といって、ギガビット伝送では考慮する必要が生じてきます。損失線路については、このコラムの最終章で触れることとします。

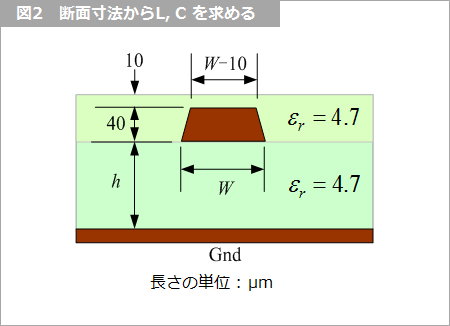
このキャパシタとインダクタを求めるにはやや難しい計算が必要ですが、伝送路の断面寸法と絶縁材の材質とが分かっていれば、解析ソフトで計算することができます。いろいろな近似式も公開されているので、比較的簡単に求めることができます。図2 のように断面寸法を与えて求めます。例として、W=100 um、h=100 umのときに、L=360 nH/m、C=119 pF/m となります。（脚注2）

このキャパシタとインダクタの値が分かったら何になるのか？それは、『特性インピーダンスって何？』で説明した特性インピーダンスと信号の伝わる速さを求めることができます。直感的には、キャパシタが大きいと、より大きな電流が流れることは容易に想像できます。大きな電流が流れるということは、特性インピーダンスが低いということです。インダクタが大きいと電流が流れにくいことも想像できます。電流が流れにくいということは、特性インピーダンスが高いということです。信号の伝わる速さは、キャパシタとインダクタが大きいほど遅く、逆に小さいほど速くなります。（脚注3）

脚注1

キャパシタはコンデンサと言ってもいいのですが、英語圏では Capacitor のほうが通じるようです。

インダクタもコイルでもいいのですが、コイルには捲線といったイメージがあるので、インダクタンスを有する素子という意味でここではインダクタといいます。

脚注2
計算ソフトはいろいろありますが、一例として以下があります。
GreenExpress V2
※ Windward 社が閉店したため、解析ツール GreenExpress V2 を入手することができません。

脚注3
特性インピーダンスは、インダクタ ÷ キャパシタの平方根で求められます。
信号の伝わる速さは、単位長（一般にはメートル）を伝わるのに要する時間（伝搬遅延といいます）の逆数です。
伝搬遅延は、インダクタ × キャパシタの平方根 で求められます。
インダクタ L=360 nH、キャパシタ C=119 pF/m とすると、

特性インピーダンス Zo = √(360 × 10^-9 ÷ 119 × 10^-12) = 55 Ω

　伝搬遅延 td = √(360 × 10^-9 × 119 × 10^-12) = 6 × 10^-9 = 6.54 ns/m

となります。
　真空中の光の伝搬遅延は 3.3 ns/m なので、ボード上を伝わる信号はおよそその倍の時間を要します。