1 円玉 2 枚を超えると集中定数回路？

部品の空間的な広がりを考える必要がない場合は回路を集中定数と考えてよく、空間的な広がりを考える必要があると分布定数とみなす必要があると『特性インピーダンスって何？』で述べました。ややこしくなるかもしれませんが、「集中定数と考えてよい」というだけで、基本的にはすべての回路は分布定数なのです。非常にゆったりした、例えば秒単位で動くような信号でも、15 センチメートル離れると、1 ns（ナノ秒）程度の時間のズレはあります。1 秒と 1 ns との間には 10 の 9 乗の違いがあるので、無視できます。
それでは、どの程度のズレになるとこの違いを気にする必要が生じるのでしょうか。一般的には、信号の立ち上がり（または立ち下がり）時間とその配線の長さとに関係します。

ここで突然ですが、用語の定義をします。図1 に示すように、信号源側のことを近端（Near-end）、信号が伝わっていく受信側（向こう側）のことを遠端（Far-end）といいます。一般的には、ドライバ側を近端、レシーバ側を遠端といいます。

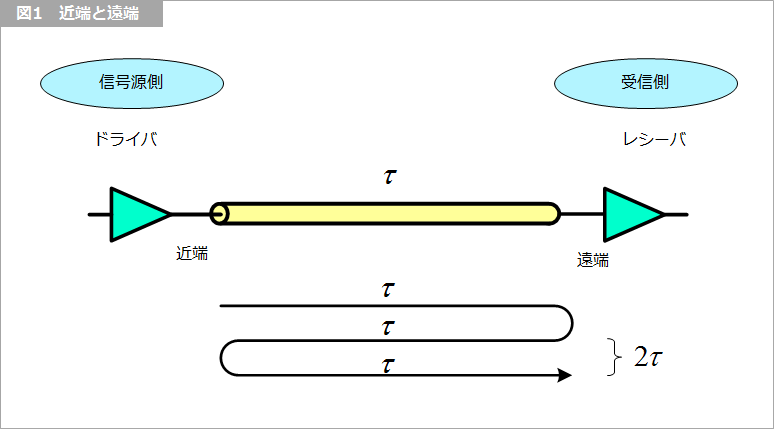
さて、信号が近端で変化して片道の時間 τ（ギリシャ文字の小文字のタウ）後に遠端に到達すると、そこで信号は反射して戻っていきます。そして信号源でまた反射して遠端に到達します。遠端で信号が反射して近端に到達し、ふたたび遠端に戻ってくる時間は信号が配線を伝わる時間 τ の 2 倍、すなわち往復時間 2τ です。近端でも遠端でも同様ですが、図2 に示すようなゆったりと変化する信号の場合には反射が戻ってきてもまだ信号は変化している最中なので、信号源は戻ってきた信号のことはあまり気になりません。同図の 3τ の点が反射の戻ってきた点です。

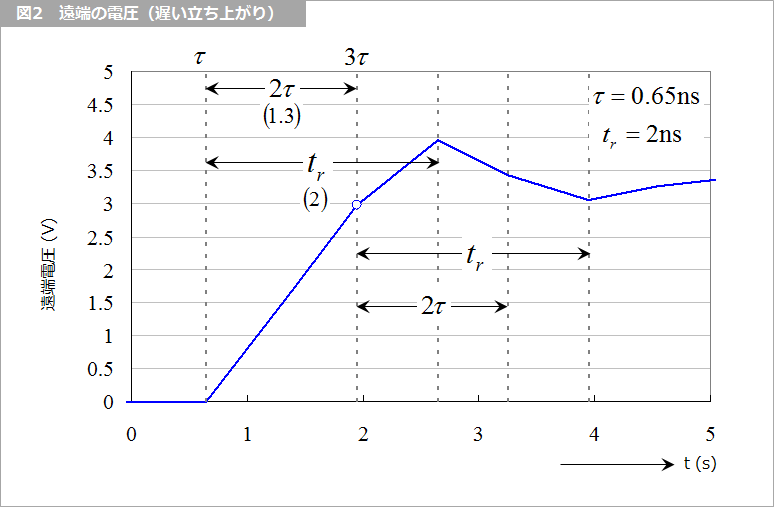
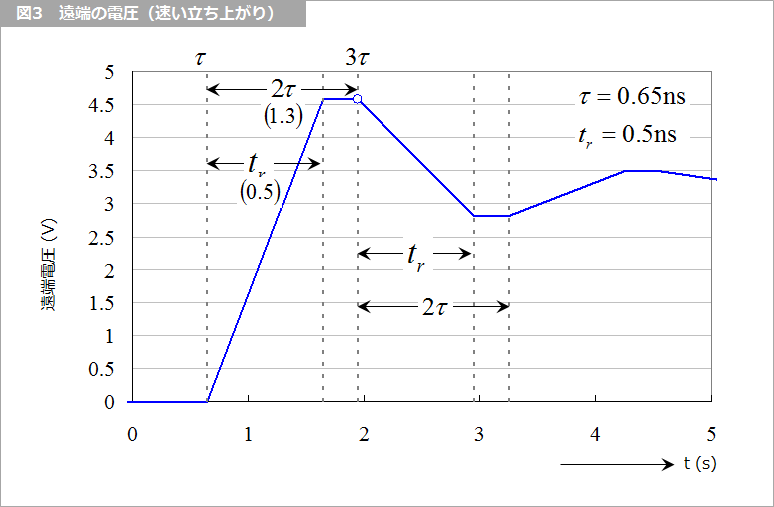
図3 に示す速い変化の信号の場合、信号が戻ってきたときにはもう次の信号の状態に変化し終わっています。同図の 3τ の点は、すでに高いレベルに変化し終わった後です。これを繰り返すことによってバタバタと暴れます。遅い変化の信号ならば、信号が戻ってきたときにはまだ変化の途中なので、変化の中に埋もれてしまい、反射の影響がそれほど顕著には現れません。厳密にいえば反射波形は存在するのですが、埋もれているので、集中定数と考えた場合と差が少ないだけです。

伝送路を伝わる信号は、光の半分程度の速度です。光は 1 メートル進むのに 3.3 ns 要しますが、電気はその倍の 6 ～ 7 ns 程度かかります。この時間を 6.5 ns とすると、伝送路の長さを x としたとき、往復に要する時間 2τ は、2τ = 6.5 [ns/m] × 2 × x [m] です。信号源の立ち上がり時間 tr を 0.5 ns とすると、2τ > tr ならば、反射が戻ってきたときには信号源はもう次の状態に変化してしまっています。式を計算すると、13x > 0.5 ですから、x > 0.5 ÷ 13 = 0.04 [m] すなわち 4 cm となります。1 円玉の直径が 2 cm ですから、これを 2 個並べた長さを超えると反射が顕在化して振動波形となる、すなわち、分布定数と考える必要が出てきて、タイトルのように「1 円玉 2 枚を超えると分布定数回路」となります。信号の立ち上がり時間が遅ければ、この境界の線長はもっと長くなることはもちろんです。

集中定数と分布定数との境界は、上にも述べたように「集中定数と考えてよい」という感覚的なものなので、およそこんなもの、といったかなりあいまいな境界と考えてください。人によっては、信号の立ち上がり時間が往復時間の 2 倍と等しいときが境界ということもあります。この場合には、1 円玉 1 枚を超えたら...となります。また、ドライバの駆動能力によってもこの感覚的な境界は変わってきます。冒頭にも述べた「集中定数と考えてよい」かどうかの境界ですから、あまり厳密に考えないようにしてください。