等価回路と方程式

反射の場合と同様に、図1の等価回路を考えます。
単一線路と比べて、線間の相互インダクタンスLMや線間容量CMが新たに加わります。

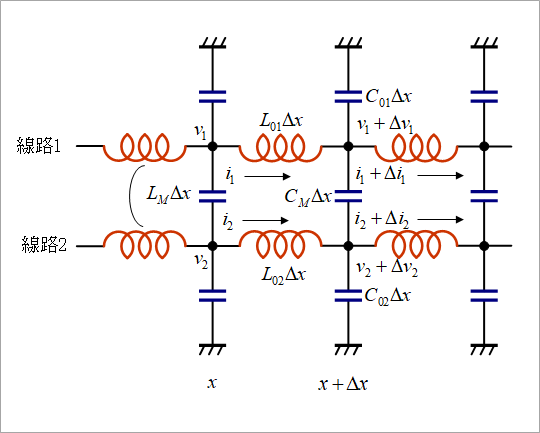
結合項を含めて、線路1に対して、式を図2 左上のように立てます。
電圧と電流の式が対称ではないので、図2の中央の矢印の式のように、C01+CM=C1、CM=-Cmと置いて、同図右のように変形します。電圧の式はそのままでもいいのですが、電流と合わせて、見やすくするため、L01=L1、LM=Lmと単純に置き換えます。

線路2に対しても同様に式を立て、反射のときと同様に、偏微分方程式を得ます。
なお、この式の変形は、必須ではありません。変形しないまま解いている例は多く見かけますが、変形したほうが簡単だと考えます。
電圧の式、電流の式それぞれを行列で表します。

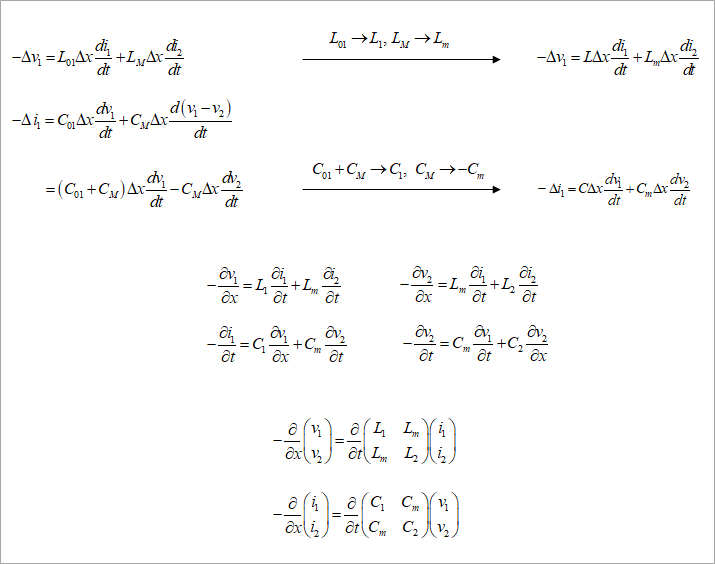
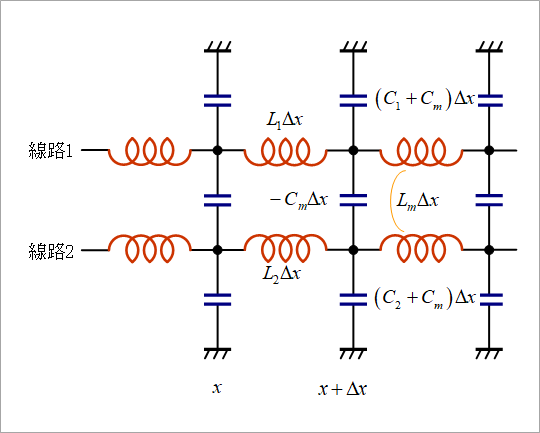
図3は、式の変形に対応した等価回路です。ここで、Cmはマイナスであることに着目してください。線路定数を求めるソフトでは、結合容量は、多くの場合、マイナスで表示します。そのマイナスの意味は、式の変形からきていると理解してください。

連立方程式から電圧を求める

図4に示すように、反射の場合と同様に、偏微分方程式をラプラス変換して、常微分方程式にします。
電圧の式を2度微分して、電流の式を代入し、電圧だけの式にします。
電圧の式のV1の2階微分をさらに2度微分して、V2の2階微分をV1の4階の微分の式に代入すると、V1に関する4階の微分方程式を得ます。

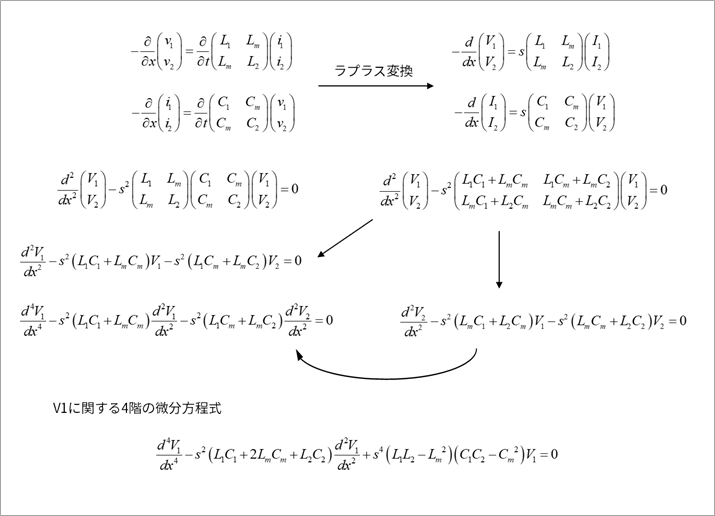
この4階の微分方程式のd/dxを微分演算子Dとおきます。(記号解法)
φ(D)は複二次式で、φ(D)=0の根の2乗(D^2)をλ1およびλ2とし、これらは、2次方程式の根の公式により、同図のように求まります。
V1は、モード1およびモード2の、二つの波動ε1およびε2の和(1次結合の最も簡単な形)で表されるとします。対称回路の場合、これらはコモンモードとディファレンシャルモードです。
ここに、λの平方根は、それぞれの波動の遅延時間で、速度uの逆数です。
モード1のε1の右辺第1項は、右行波(右に進む波)で、第2項は左行波です。係数のA11およびA12は積分定数で、後で、境界条件により求めます。
V1の式を、モード1とモード2の1次結合として、a11とa12の係数(ここでは、いずれも1)をかけて表現します。

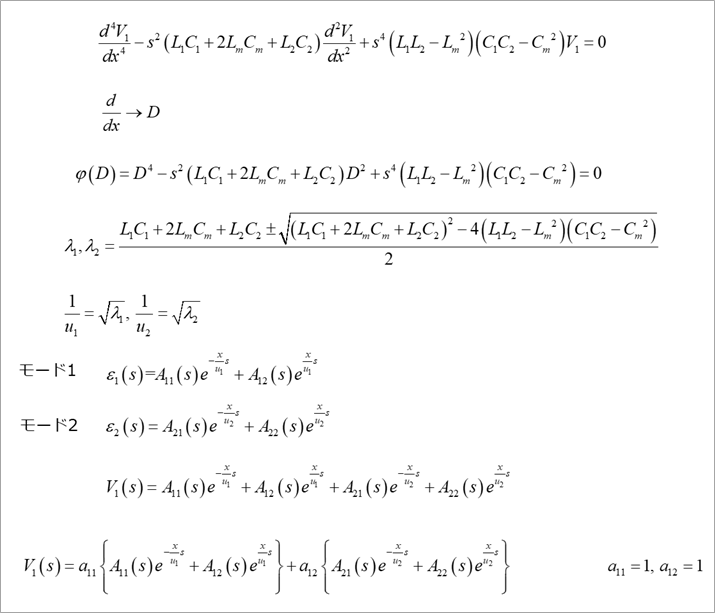
図4のV1の2階微分の式から図6に示すように、V2を求めます。
この式に、図5の最後のV1の式と、V1の2階微分とを代入するとV2が求まります。
この式も、ε1とε2との1次結合です。それぞれの係数を、同図のように、a21とa22とおきます。

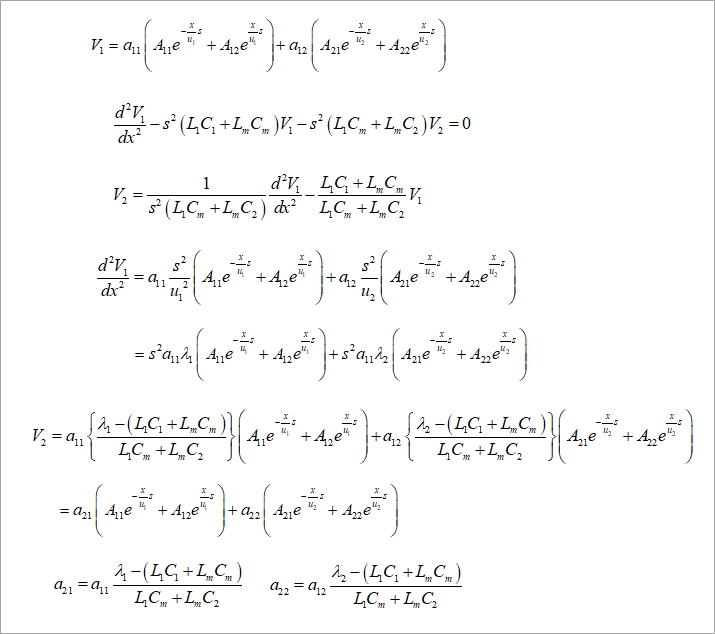
電流を求める

図7に示すように、電圧の式から電流を求めます。
図4の電圧の式から電流を求めます。この式中の電圧の微分を求めます。
この微分の式を上で求めた電流の式に代入して、I1およびI2を求めます。
電流も、電圧と同様に、モード1とモード2の1次結合として表されます。これらの式の左辺の文字は、ギリシャ文字のι(イオタ)です。

図8の回路に対して、近端と遠端の電圧、電流を図のように決めると、電圧と電流の関係は、図に示すようになります。

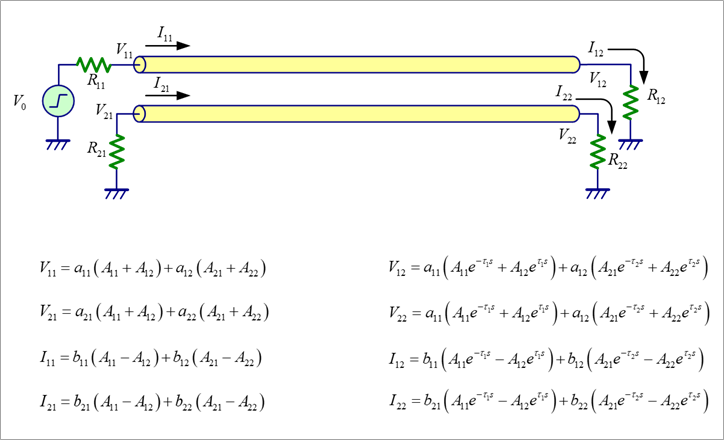
境界条件により積分定数を求める

図9に近端と遠端の境界条件を示します。これらの4つの式に、図8の電圧と電流の式を代入すると、4つの積分定数、A11、A12、A21、A22に関する連立方程式が求まります。

このA11～A22についての連立方程式を解いて、図8の式に代入すると、近端と遠端の電圧が求まります。
今回は、連立方程式を立てるとこまでとします。

4元の連立方程式なので、それほど簡単ではないですが、解を、ラプラス逆変換すると時間関数を得ます。
対称線路については拙著を参照ください。

次回は、いくつかの解き方について述べる予定です。