表面層と中間層の遠端クロストーク

遠端クロストークは、表面層と中間層とで形状が異なります。図1(a) に中間層の遠端クロストークの例を示します。

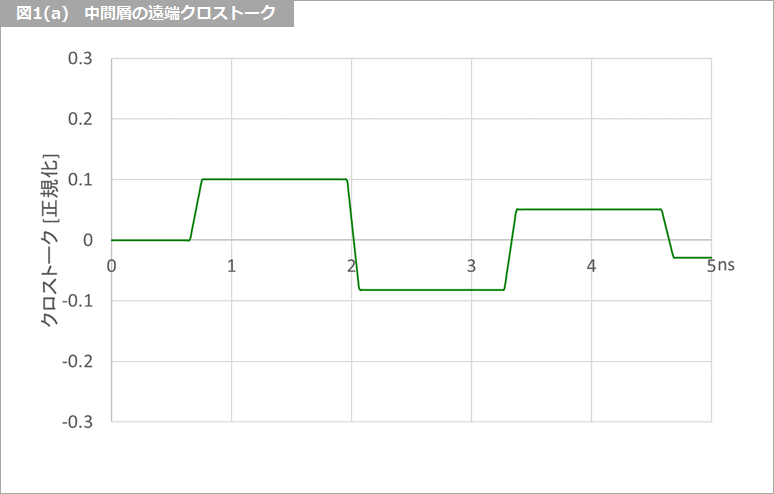
クロストークの形状は、近端クロストークに似ています。このクロストークを、仮に「骨格部」と名付けます。ここだけの名前で、一般性はないのでご注意ください。図1(b) に表面層の遠端クロストークの例を示します。これは、図1(a) の骨格部に 図1(c) のひげ状のクロストークが重畳した形、すなわち、(b)=(a)+(c) です。

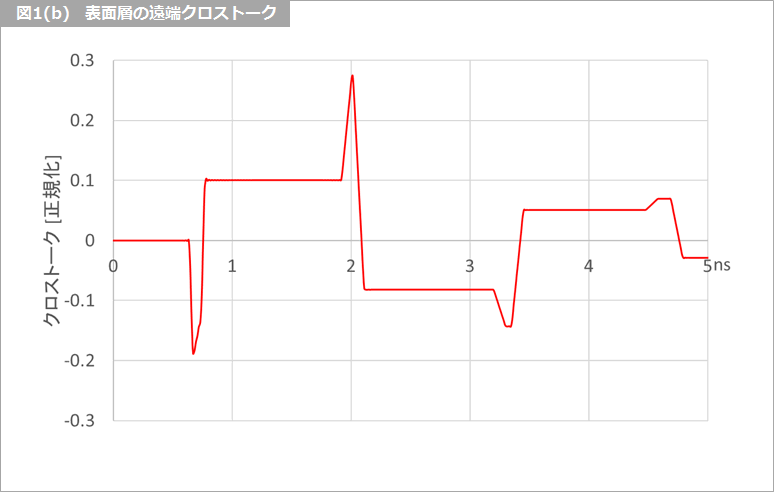
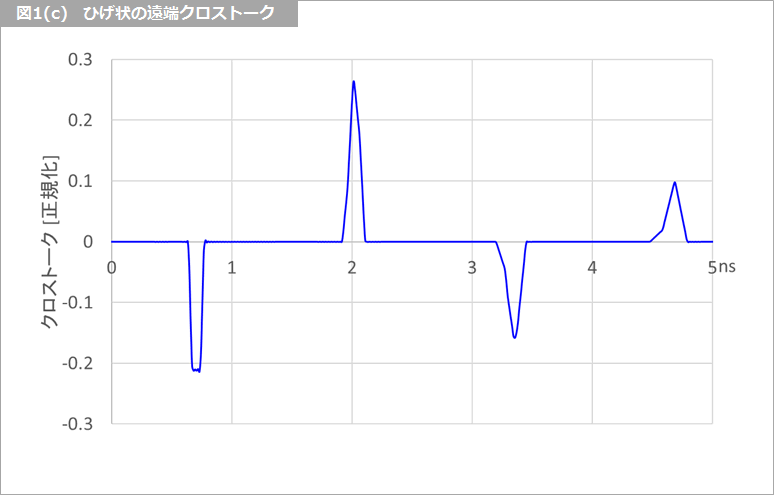
骨格部とひげ状のクロストーク

骨格部は、ドライバの駆動能力に対して、『近端クロストークとその対策』の 図5 に示すような特性を示します。『バックワード・クロストーク係数 Kb とフォーワード・クロストーク係数 Kf』で述べたように、終端抵抗を R = √ZC×ZD に選ぶとゼロにすることができます。ひげ状のクロストークは、コモンとディファレンシャルの二つのモード τC と τD の遅延時間の差 Δτ によって生じます。（τ：ギリシャ文字小文字のタウ）

ひげ状のクロストークについては、『バックワード・クロストーク係数 Kb とフォーワード・クロストーク係数 Kf』の 図4 を参照ください。また、信号の立ち上がり時間 tr にも関係して、tr が Δτ より小さい場合には、そのピークは、信号の 1/4 になり、tr が Δτ より大きい場合には、tr に反比例します。

整理すると、以下のとおりです。

• 骨格部はドライバの駆動能力によって変化
• ひげ部は τC、τD、tr に依存

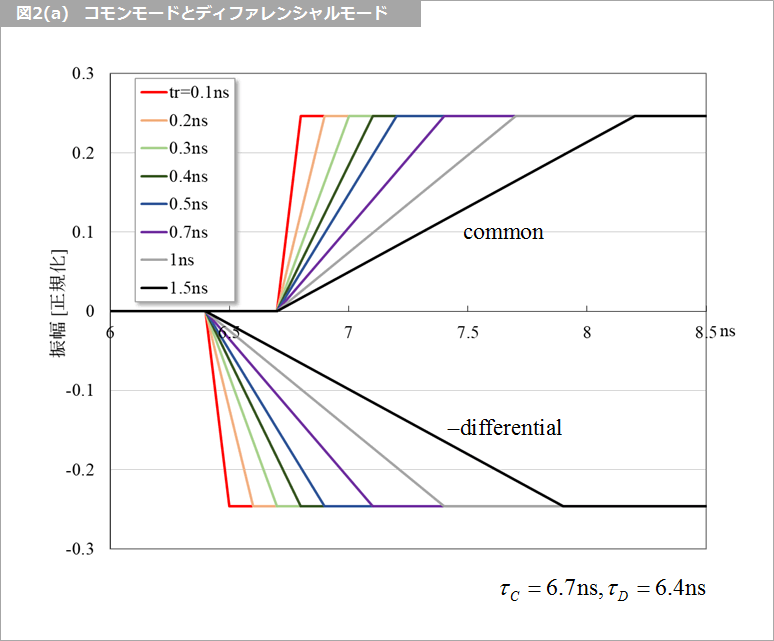
図2(a) は、信号の立ち上がり時間trを変化させたときの、コモンとディファレンシャルの波形を示します。振幅は、『バックワード・クロストーク係数 Kb とフォーワード・クロストーク係数 Kf』の 図2 と同じく、コモンは 1/2 と 1/2、ディファレンシャルは、1/2 と -1/2 です。

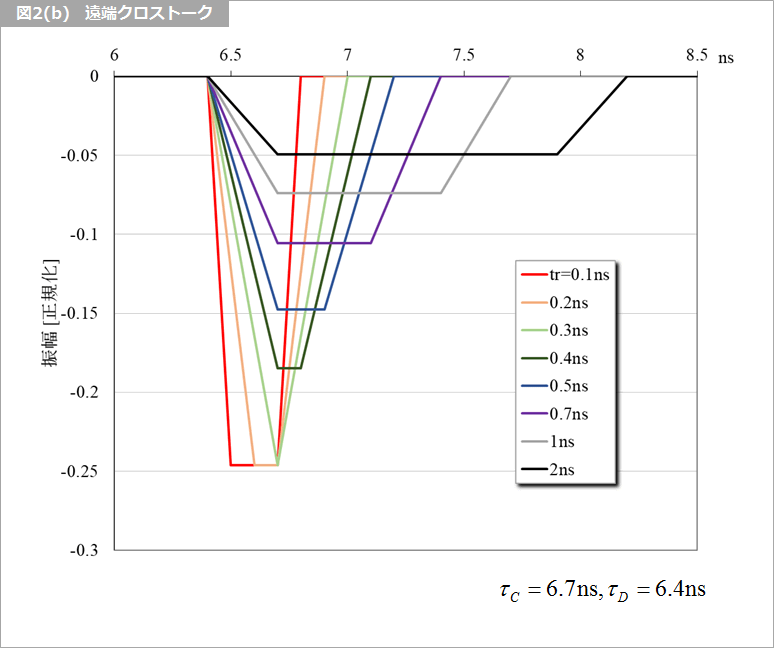
図2(b) は、コモンとディファレンシャルの和、すなわち、『バックワード・クロストーク係数 Kb とフォーワード・クロストーク係数 Kf』の 図3 の被害者線路の波形を示します。この図では、τC と τD との差は 0.3ns なので、tr = 0.3ns 以下では、遠端クロストークは、-0.25 となります。『バックワード・クロストーク係数 Kb とフォーワード・クロストーク係数 Kf』の 脚注3 も参照ください。

ひげ状のクロストークの負荷容量の影響

中間層の遠端クロストークは骨格部だけでひげ状のクロストークは生じないと述べましたが、実は、近端や遠端の静電容量によってひげが生じることがあります。静電容量と特性インピーダンスや終端抵抗による時定数によって波形が指数関数的になまります。遠端ひげ状のクロストークは、コモンとディファレンシャルの遅延時間の差によって生じるので、負荷容量に対して、特性インピーダンスが大きいほうが時定数が大きいので、遅延が大きくなります。この遅延の差によって、τC と τD とに差が生じてひげ状のクロストークが生じます。

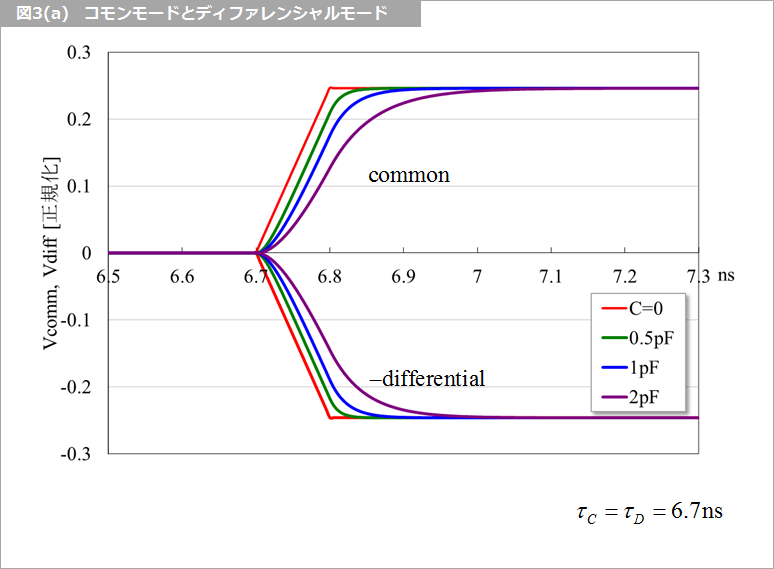
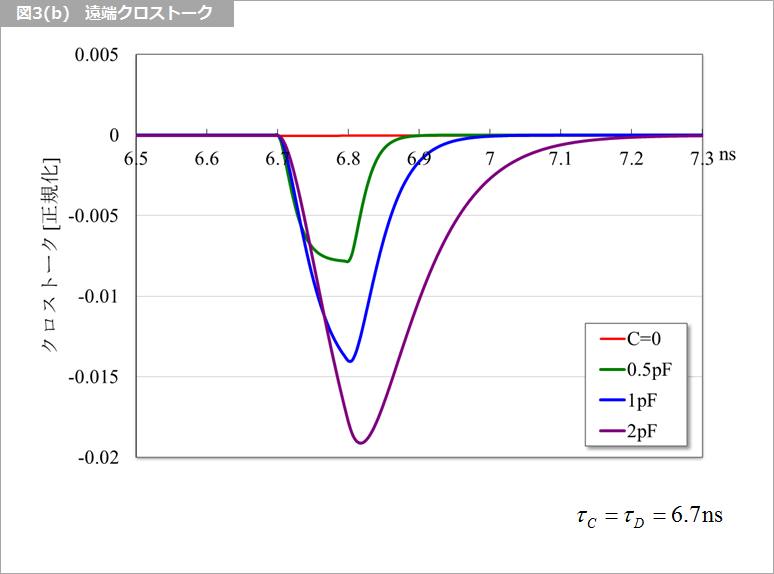
図3(a) は、遠端の静電容量を変化させたときのコモンとディファレンシャル（負）の波形です。上下対称に見えますが、両者の和は、図3(b) のようになり、τC と τD に差があるときのようにひげ状の遠端クロストークが生じます。これは、差動クロストークの厳密解（リンク）の容量特性と同じ現象です。