反射波形の解析

反射波形の解析については、以下の方法を述べてきました。

■ IBISを用いた反射の解析～その1、その2
　 https://www.macnica.co.jp/business/semiconductor/articles/basic/111905
　 https://www.macnica.co.jp/business/semiconductor/articles/basic/112009

■ バージェロン図表
　 https://www.macnica.co.jp/business/semiconductor/articles/basic/122501

■ 非線型バージェロン図表
　 https://www.macnica.co.jp/business/semiconductor/articles/basic/122797

■ 格子線図
　 https://www.macnica.co.jp/business/semiconductor/articles/intel/122061

微分方程式による解法

ここでは、原点に戻って、等価回路から方程式を立てて、微分方程式を解く方法を述べます。

数式は敬遠しがちですが、少し冗長であるくらいに詳しく述べますので、敬遠しないで、読んでください。数式に強い方は、少し斜め読みでも理解できると思います。

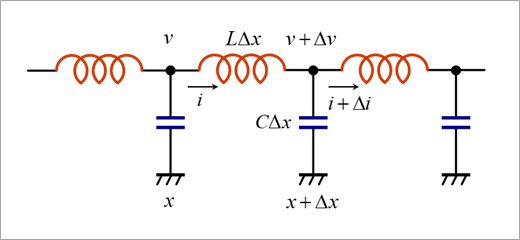
図1は、分布定数回路の等価回路です。名前のとおり、回路定数が分布的に接続されています。回路定数は、キャパシタとインダクタです。

以下も参照ください。
『分布定数回路～何が分布しているのか？』
https://www.macnica.co.jp/business/semiconductor/articles/basic/110389

さらに、キャパシタには漏れコンダクタンスGが並列に、インダクタには抵抗Rが直列に存在しますが、ここではこれらは無視します。図中の、キャパシタは、CΔx、インダクタは、LΔxですが、CとLは、単位長(メートル)当たりの値なので、微小区間Δxを掛けています。Δxは、具体的な値は定義しなくで、微小区間と考えてください。微分のd/dxのdxと同じです。

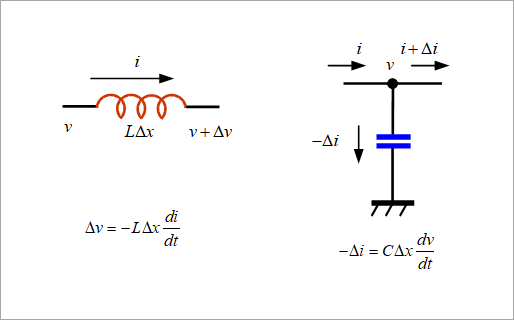
図2は、インダクタとキャパシタの、電圧と電流との関係です。インダクタの電圧降下は、インダクタと電流の微分との積です。電圧降下なので、負号がつきます。キャパシタの電流の式は、あまり馴染みがないですが、電荷=キャパシタ×電圧の両辺を微分したものです。電荷の微分は電流です。言い換えると、電流の積分が電荷です。

図3は、図2のインダクタの電圧とキャパシタの電流の式を変形して、微分方程式する過程を示します。

まず、式(1)および式(2)の両辺をΔxで割り、Δxを無限小にすると、式(3)と式(4)の微分になります。なお、独立変数が、距離xと時間tの二つがあるので、偏微分となります。
式(3)の両辺をxで微分して式(5)を得ます。
式(5)の右辺の、電流のxによる微分は、式(4)と同じなので、式(4)を代入して式(6)を得ます。
式(6)を、波動方程式といいます。
式(6)に、ラプラス変換を施します。

ラプラス変換は、微分方程式を算術方程式に変換するもので、d/dtはsと置くだけです。これにより、偏微分方程式を常微分方程式(7)に変換できました。
式(7)は、最も簡単な2階の線形微分方程式です。

その解は、二つの積分定数を、A1、A2として、式(8)のようになります。

次に、図4で電流を求めます。
式(3)の偏微分をラプラス変換して、式(9)を得て、式(10)の電流Iを求めます。
式(8)をxで微分して、式(11)を得ます。
式(11)のdV/dxを式(10)に代入して、式を順次変形して、式(12)を得ます。ここに、特性インピーダンスZ0を、式(13)のように定義します。

境界条件

二つの積分定数は、近端と遠端の電圧と電流の関係から求めます。図5の式(14)は近端における電圧と電流の関係、式(15)は遠端における条件です。

図6に、近端の境界条件から、二つの積分定数A1およびA2に関する方程式を導き出します。まず、近端の境界条件の式(14)のV(x,s)とI(x,s)それぞれにx=0を代入します。

電圧Vは、式(8)にx=0を代入して、式(16)を得ます。
電流Iは、式(12)にx=0を代入して、式(17)を得ます。

式(16)と式(17)を式(14)に代入した式(18)を、A1とA2について整理して、式(19)を得ます。これが、A1とA2についての連立方程式の一つです。

図7に、近端と同様に、遠端の境界条件からA1とA2に関する、もう一つの方程式を導き出します。遠端の境界条件の式(15)のV(x,s)とI(x,s)それぞれにx=l(エル)を代入します。

電圧Vは、式(8)にx=lを代入して、式(20)を得ます。
電流Iは、式(12)にx=lを代入して、式(21)を得ます。

ここに、√LC×lは、近端から遠端までの信号の遅延時間τです。式(20)と式(21)を式(15)に代入した式(22)を、A1とA2について整理して、式(23)を得ます。これが、A1とA2についての連立方程式の他の一つです。

図8の式(19)と式(23)がA1とA2についての連立方程式です。2元(未知数が二つ)の連立方程式なので、簡単に解けると思いますが、復習の意味で、付録に記載しました。
行列の形にして、Sarrusの方法で解くのが、特に数値計算では簡単でしょう。

式(24)は、式(19)と式(23)を行列の形に書き直したものです。
式(25)は、式(24)の係数の行列式Δです。
式(26)、式(27)がこの連立方程式の解です。

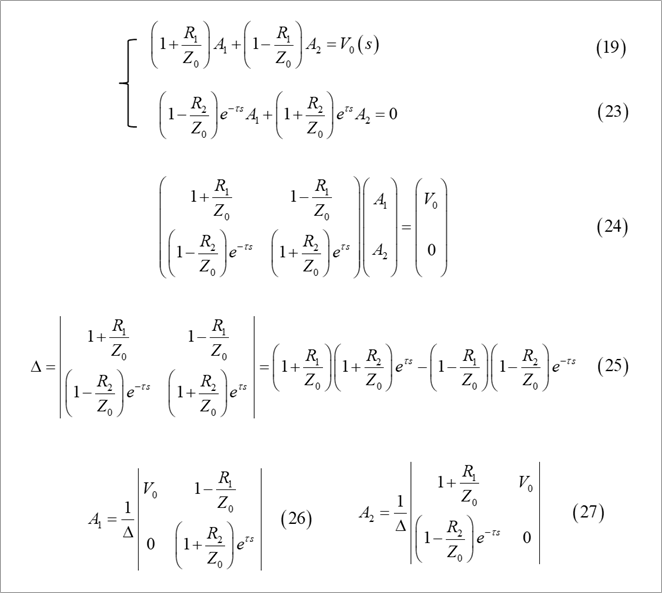
図9に、式(26)、式(27)を整理して、式(28)、式(29)に書き直して示します。ここに、式(30)と式(31)は、それぞれ、近端と遠端における反射係数です。
反射係数については、

『反射係数』
https://www.macnica.co.jp/business/semiconductor/articles/basic/132300
を参照ください。

式(28)、式(29)を、遠端の電圧、式(20)に代入して、式(32)を得ます。
式(32)は、ラプラス変換した式なので、これをラプラス逆変換すると、時間関数になります。

ラプラス変換については、

『ラプラス変換とフーリエ変換』
https://www.macnica.co.jp/business/semiconductor/articles/basic/128001
も参照ください。

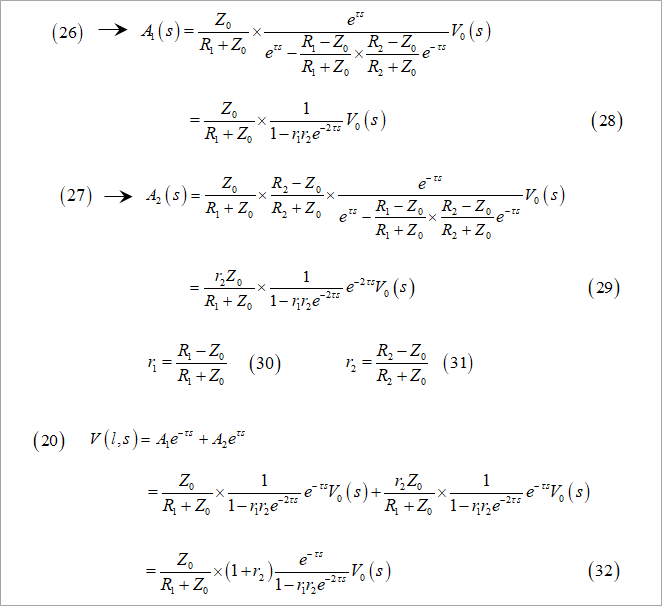
図10は、上の記事の図2 のラプラス変換の公式を再掲したものです。

図9の式(32)は、図10の公式に変換式がありません。式(32)の分数は、図11の式(33)のように級数展開できます。無限等比級数の和の公式です。そこで、式(32)を書き換えると、式(34)を得ます。同式の{ }内は、図10の右の一番上の変換(時間遅れ)、式(35)です。

この公式を用いて、式(34)をラプラス逆変換すると、式(36)となります。τの奇数倍遅れのドライバの出力波形に、反射係数r1r2を順次掛けて加えます。

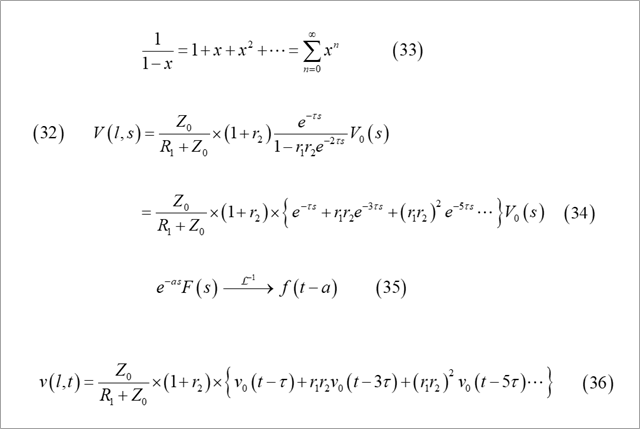
図12に、式(36)の計算結果の例を示します。反射を誇張するために、R1=11Ω(24mAドライバ相当)とし、τ=0.35ns(5cm程度)としました。ステップ波形は、立ち上がり時間がゼロの場合、ランプ波形は、立ち上がり時間が0.5ns(0%-100%)としました。それぞれ、τ、3τ、5τ...遅れに反射係数r1r2を掛けた波形を図の左に、それらを時間軸上で加えたものを図の右に示します。

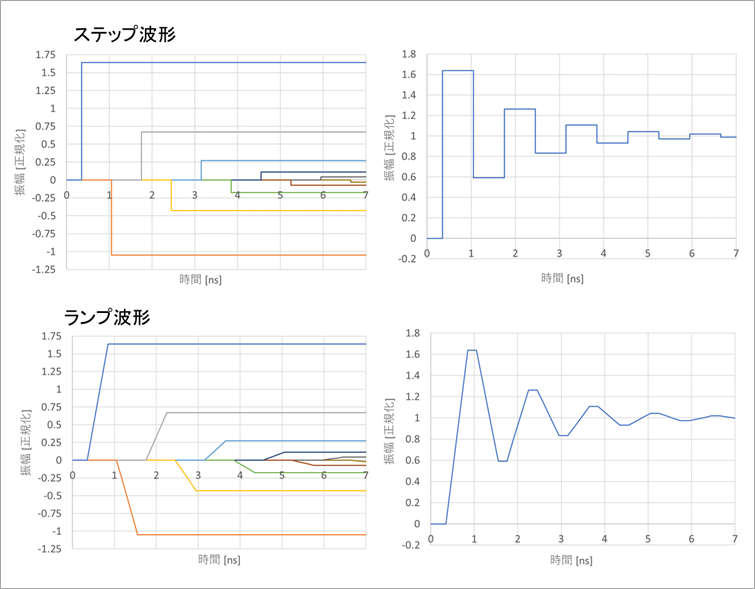
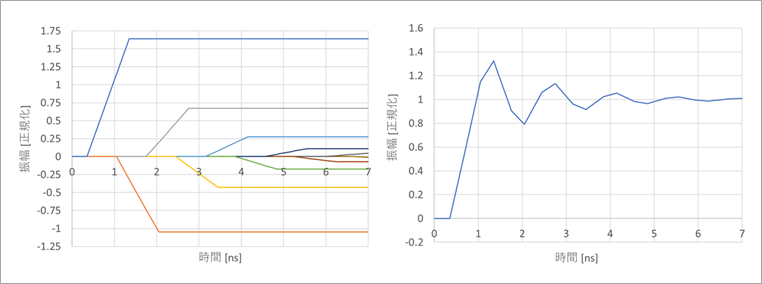
図13に、立ち上がり時間を1nsとした場合の計算結果を示します。立ち上がり時間trと往復時間2τとの大小関係で、反射波形がフル振幅まで到達してないことが分かります。図12と比較してください。

付録

変数が二つ(2元)の連立方程式の解き方を復習します。

式(1)および式(2)の、未知数が、xとyの連立方程式を解きます。まず、yを消去するために、式(1)の両辺にEを掛け、式(2)の両辺にBを掛けて、式(3)、式(4)を得ます。式(3)と式(4)の両辺を引くと、yの項が消えて、式(5)となり、これから、式(6)のようにxが求まります。

同様に、式(1)にDを掛け、式(2)にAを掛けて辺々引き算すると、式(9)となり、式(10)のyが求まります。これで目的は達したのですが、行列式を使った方法を紹介します。式(1)、式(2)の連立方程式を、式(11)のように行列で表します。式(12)は、式(11)の係数の行列式Δです。xは、式(11)の1列目を、右辺の行列と置き換えて、行列式を計算して、係数の行列式Δで割って求めます。yも同様に、式(11)の2列目を右辺の行列と置き換え、行列式を求めてΔで割ります。行列式の計算は、3×3までは、式(15)のSarrusの方法(たすき掛けの演算)で、右下がりの掛け算をプラス、左下がりの掛け算をマイナスにして加算します。