線型の特性と非線型の特性

『バージェロン図表』では、出力抵抗や終端抵抗が線型の場合でした。線型だったので、基本的には連立一次方程式を解きました。しかし、実際には、『IBISモデルを用いた反射の解析 ～その2』に述べたように、ドライバの特性は非線型です。非線型の場合には、IBIS のように数値で与えられた曲線同士の交点を求める必要があります。

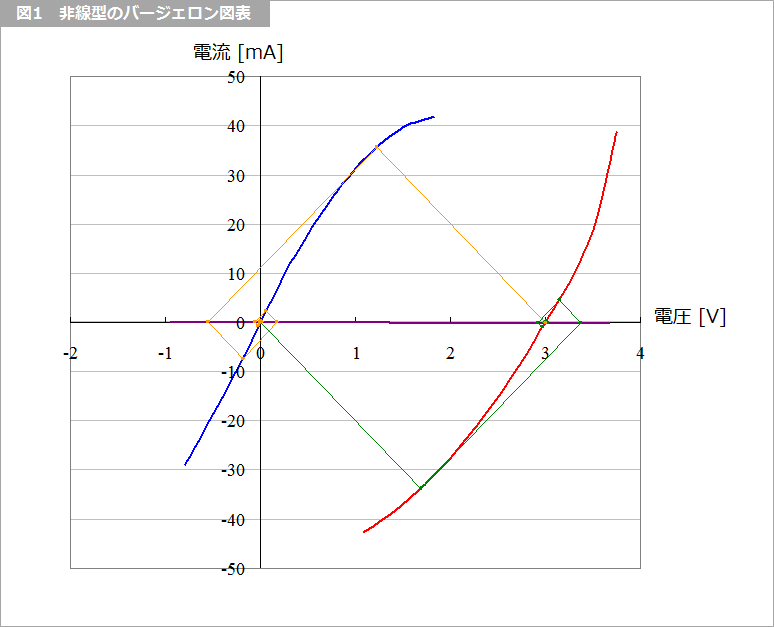
図1 は、IBIS によって求めたドライバの出力特性を用いたバージェロン図表です。手書きでこれを描くのは、精度は別にすればそれほど難しくはありません。

一方、エクセルでは、原点を通る傾きが -1/Z0 の緑色の直線が、Pull Up の赤い曲線と交わる点を数値的に求める必要があります。

2本の曲線の交点を求める

まず、図2 に示すような原点を通る傾きが -1/Z0 の緑色の直線と、Pull Up の赤い曲線との交点を求めます。

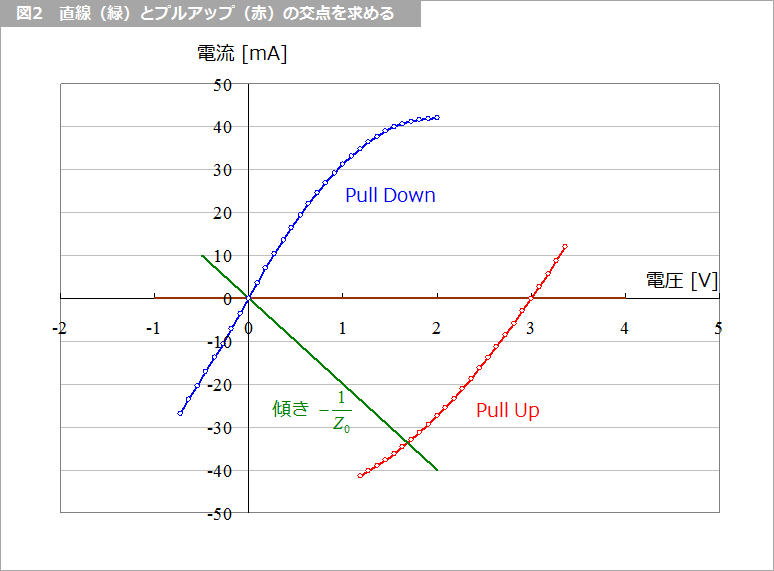
そして、図3 に、図2 の交点付近を拡大して示します。Pull Up の横軸（電圧）と縦軸（電流）は、それぞれ数値で与えられています。傾き -1/Z0 の直線は式で与えられるので、Pull Up の電圧に対して電流を求めることが出来ます。

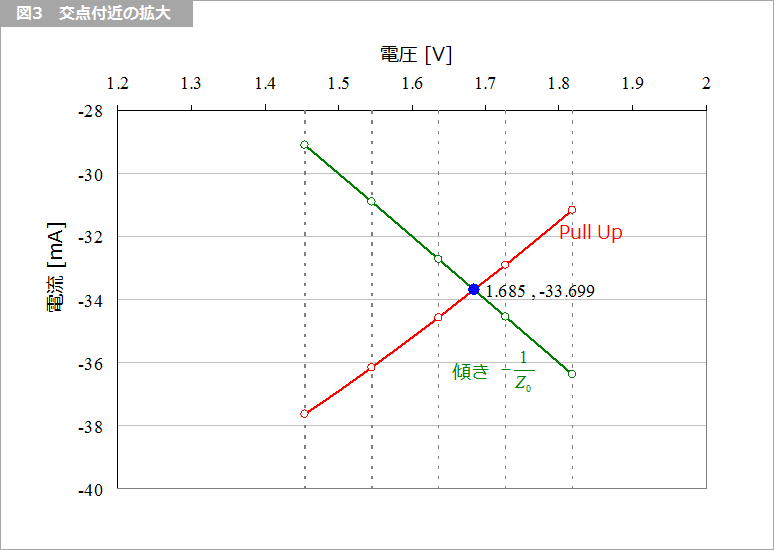
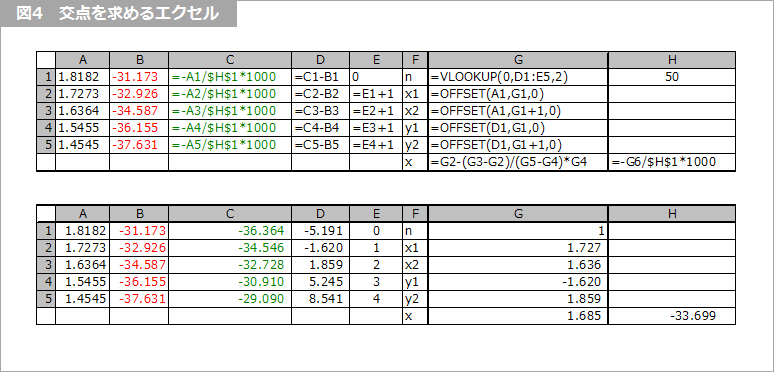
図4 はそのエクセルシートです。上に式を、下に数値を示します。A列は Pull Up の電圧を、B列は同じく電流を示します。実際には IBIS データなので、もっと広い範囲のデータです。（脚注1）

C列は緑の直線の式で、A列の電圧に対して電流を求めています。ここでは 1000倍して、電流を mA で表しています。H1 に特性インピーダンスZ0を与えています。

交点は、この曲線と直線との差がゼロになる点を求めることを意味します。D列はこの差です。ここで重要な条件は後述しますが、差が昇順になるように引き算の向きを選択することです。

Vlookup 関数

ゼロになる点を求めるのは、Vlookup 関数を用います。この関数は、

VLOOKUP(検索値, 範囲, 列番号, [検索の型])

で、検索値は 0（ゼロ）で、範囲で示した左端、この場合は D列を検索します。列番号は、検索した場合に返す列を、左端の列を含めた列番号で示します。列番号を 2 とすると、検索値がみつかったら E列の値が返されます。図4 に示すように E列に 0 から 1 ずつ増加する数値を入れておくと、範囲で指定した行から何番目の行かが分かります。

検索の型は TRUE を指定するか省略すると、検索値が求まらない場合は、検索値未満で最も大きな値を使用します。TRUE の場合には、検索列は昇順に並べておく必要があります。検索の型が FALSE の場合、検索値と完全に一致する値だけが検索され、見つからない場合はエラー #N/A となります。今回は、

VLOOKUP(0, D1:E5, 2)

なので、D1:E5 の範囲で、左端の列は D列なので、ゼロ未満で最も大きいものは、-1.62 で、2番目の列の E1、すなわち 1 を返します。

Offset 関数

G2 と G3 は、0 未満で最も大きい -1.62 とその次に大きい 1.859 を、すなわち、0 を挟んでその前後の横軸（電圧）を見つけます。ここの関数は、『バージェロン図表』でも用いた Offset 関数（豆知識：Offset 関数 参照）です。

Offset の基準は A1 で、G2 はそこから G1、すなわち 1 だけ下のセル、すなわち A2 となります。G3 はさらにその下、すなわち A3 です。G2 と G3 は A2 と A3、すなわち横軸なので、x1=1.62、x2=1.859 と置きます。G4 と G5 は、G2 と G3 に対応する縦軸なので、Offset の基準を D1 として、D2 と D3 となります。G4 と G5 は縦軸なので、y1=-1.62、y2=1.859 と置きます。

交点の座標

縦軸 y がゼロになる点を挟んで 2点が求まったので、この 2点を通る直線が y=0 になる x を求めます。この 2点を通る直線は、

x=x1+(y2-y1)/(x2-x1)*(y-y1)

となり、y=0 を代入すると、x が求まります。（脚注2）
これが、G5 の式で、電流は H5 で求まります。これを順次繰り返すと、IBIS データのような非線型の特性の場合のバージェロン図表を求めることが出来ます。

今回は、2つの線のうち、一方が式で与えられた直線なので比較的簡単でしたが、両方が数値で表された線の場合は、少し複雑になります。本論から少し外れるので、希望者が多ければ機会をみて触れたいと思います。

脚注1
IBIS の仕様では、100行以下で表すことになっています。

脚注2
数学の授業では、

y=y1+(y2-y1)/(x2-x1)*(x-x1)

と習いました（のはず、筆者にとっては半世紀以上前のことなので）が、今回は x を求めたいので、x= の式になります。