差動クロストークの近似解
差動クロストークについては、『差動クロストーク』で基本的な特性を述べました。その際に、ドライバの特性(出力抵抗)によって、クロストークの現れ方が異なることを示しました。
差動クロストークは、ドライバが電圧源や電流源の場合に大きく、整合ドライバの場合にはほとんど生じません。したがって、差動クロストークが問題になるような場合には、整合ドライバが主に用いられます。整合ドライバの代表は CML (Current Mode Logic) ですが、電流源ドライバの LVDS (Low Voltage Differential Signaling) も、最近は、出力抵抗を整合させる例が多いようです。
差動クロストークの厳密解
その後の解析により、ドライバやレシーバの静電容量が大きく差動クロストークに影響を及ぼすことが分かりました。また、クロストーク係数や線長による影響も明らかになりましたし、表面層と中間層とで、その性質に差があることも分かりました。以下に、差動クロストークに影響を与えるパラメータとその特性について述べます。
ペア間(チャネル間)のクロストーク係数の影響
シングル伝送の場合には、クロストークを低減させるために、2本の線路の線間を広げて、クロストーク係数を小さくすることが対策の基本でした。
差動伝送の場合には、ペア内の線間距離は、特性インピーダンスの要求により決まります。ペア間のギャップは、直感的には、広げるほうがクロストークは小さくなると思われますし、実際にもほとんどそのとおりです。ただし、表面層では必ずしもこの傾向は成り立ちません。
図1 の回路において、ペア間、すなわち、線路2 と線路3 とのクロストーク係数を ξ23 (ξ:ギリシャ文字小文字のクサイ)として、差動クロストーク v32-v42 を求めます。
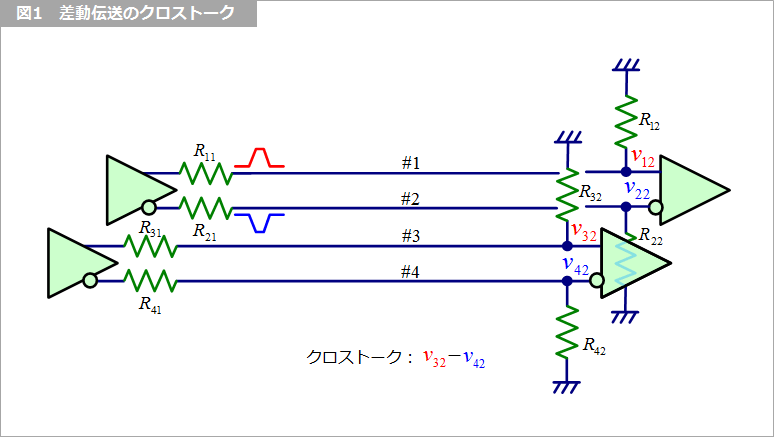
図2 に、ξ23 に対する差動クロストークを示します。図2 凡例に示す「表」、「中」はそれぞれ表面層、中間層を意味し、「近」、「遠」は近端および遠端を意味します。「表・遠」すなわち表面層の遠端は、ξ23 が 0.1 付近で最大となり、0.25 付近で最小となりました。近端は、表面層、中間層ともに ξ23 にほぼ比例し、中間層の遠端は、振幅は極めて小さいですが、ほぼ ξ23 の 2乗に比例します。
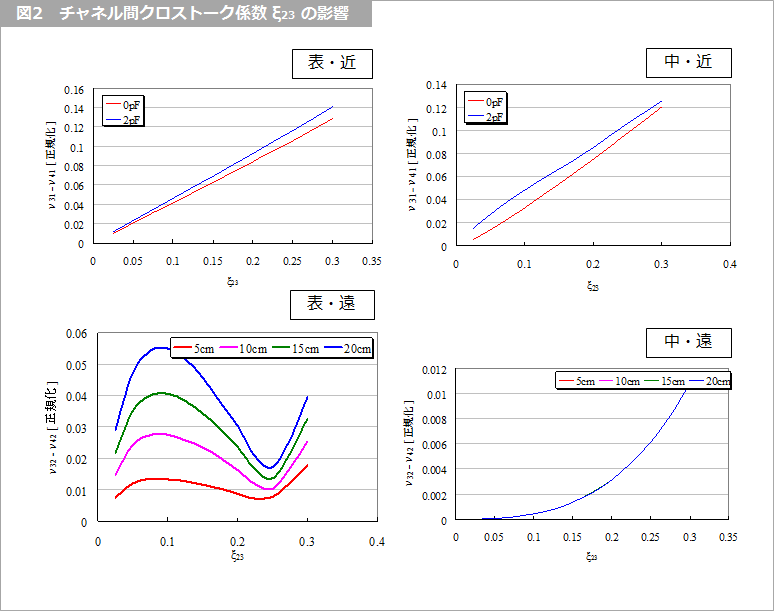
線長の影響
4本線路には、それぞれの特性インピーダンスと遅延時間を持つ 4つの伝搬モードが存在します。それぞれの線路の電圧と電流は、これらの伝搬モードの1次結合(>脚注1)で表されるので、各モードの伝搬遅延が異なると、ひげ状のクロストークになって現れます。
中間層では、全ての伝搬モードの遅延時間は等しいが、表面層では基本的に全て異なる遅延時間を有します。このため、図3 に示すように、中間層のクロストークは線長に無関係ですが、表面層ではクロストークは線長に比例します。
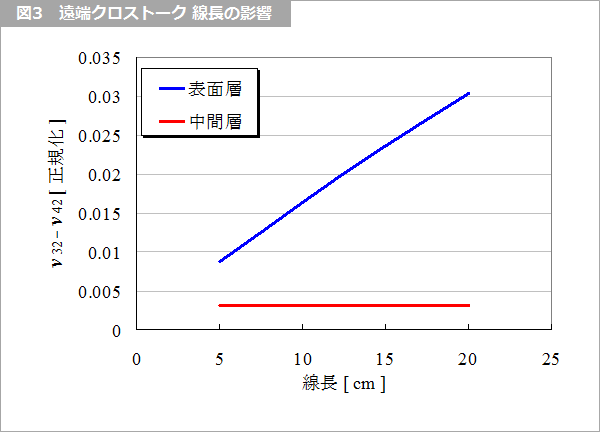
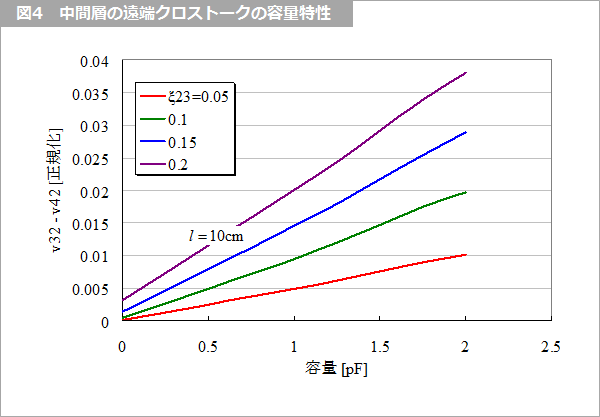
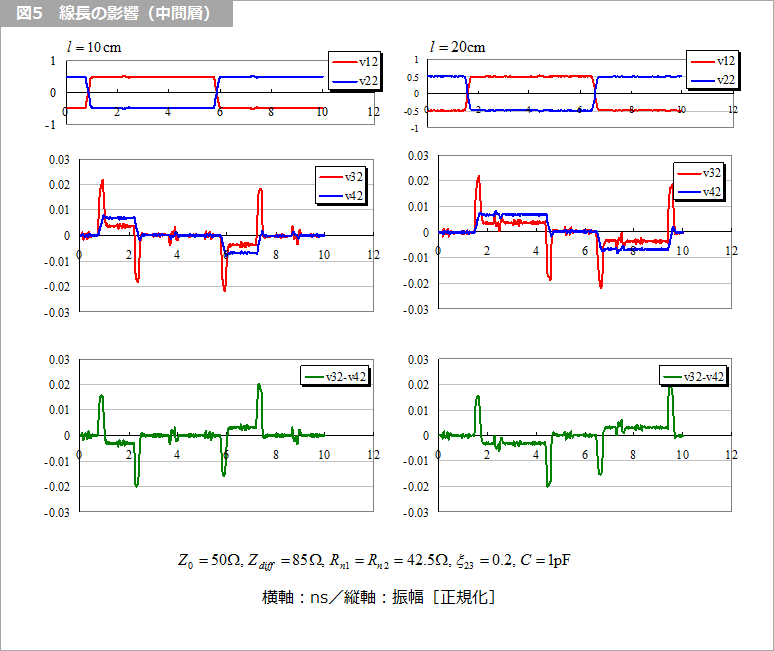
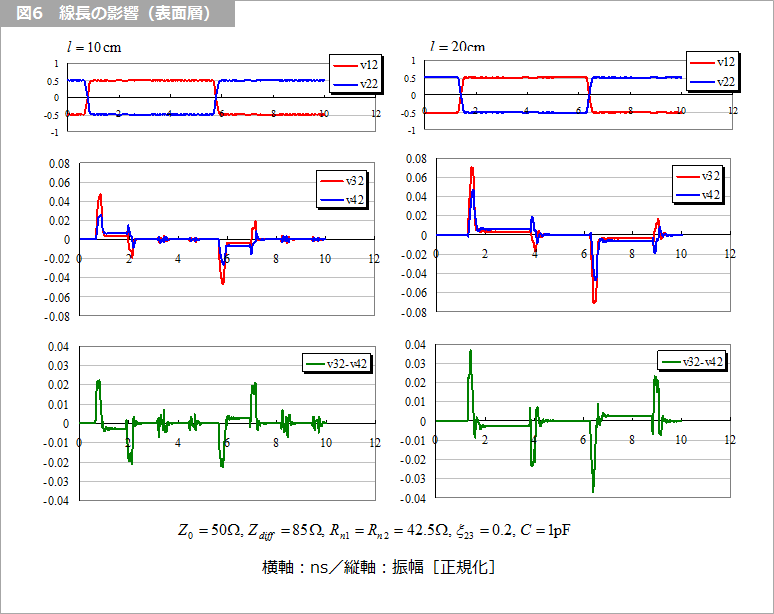
図5 および 図6 は、線長の違いによるクロストークの解析例を示します。上に述べたとおり、中間層は線長に無関係ですが、表面層は線長に比例していることが分かります。なお、近端は、表面層、中間層ともに、線路の往復時間が、信号の立ち上がり時間より小さい場合を除いて、線長には依存しません。
近端、遠端の容量の影響
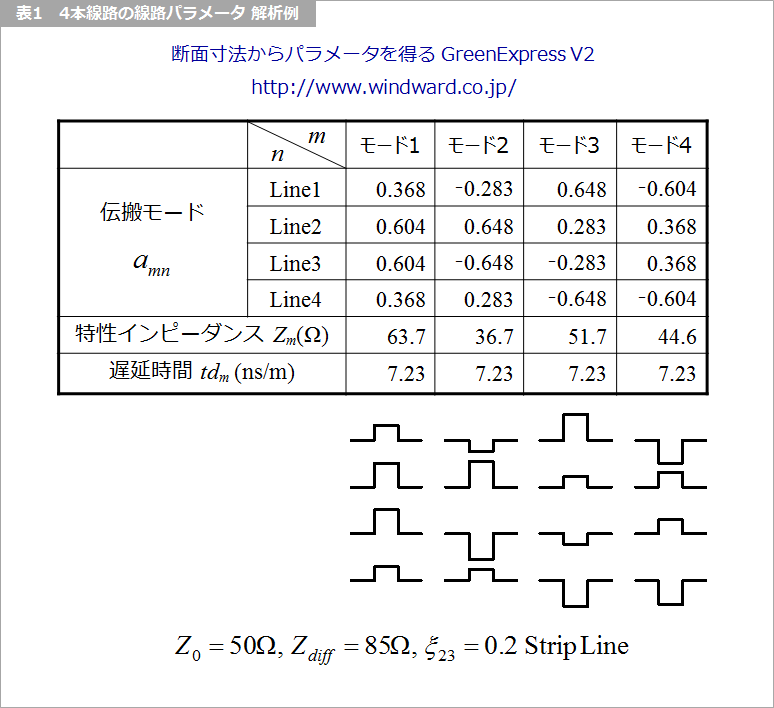
これまでは、ドライバやレシーバの静電容量についてはあまり考慮されてきませんでした。容量の影響について述べる前に、表1 に、ある 4本線路の各伝搬モードの特性インピーダンスとそれぞれのモードの係数の例を示します。近端、遠端の容量と特性インピーダンスによる時定数によって、立ち上がり波形がなまります。そのなまり方は、特性インピーダンスが大きなモードほど顕著です。
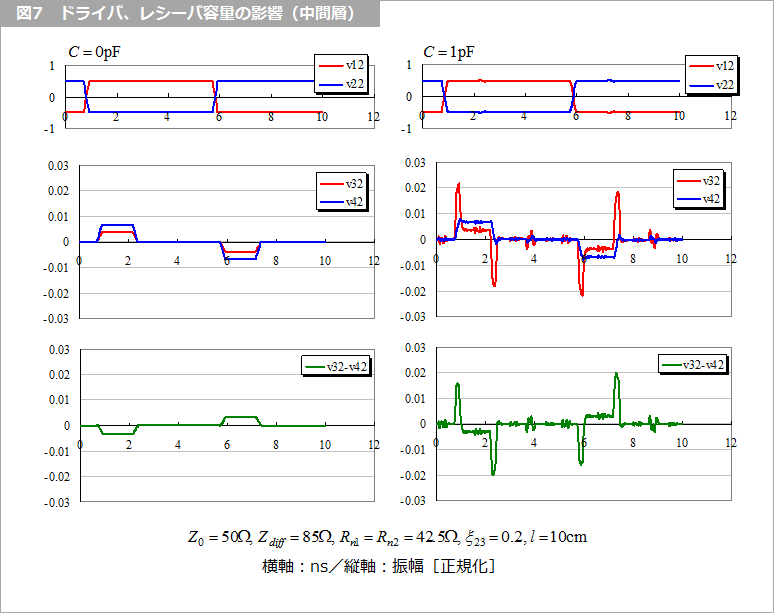
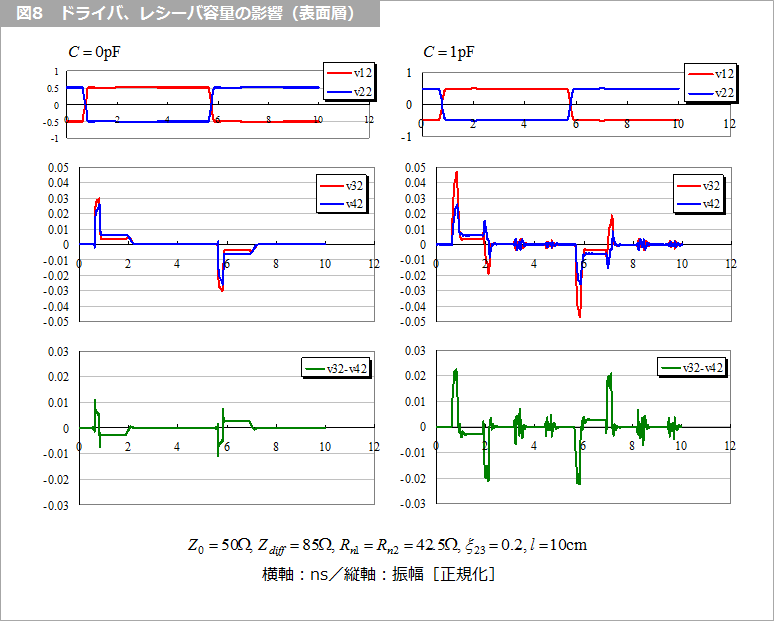
また、各モードの振幅も異なるので、これらの 1次結合によって遅延時間の差が「ヒゲ状」のノイズとなります。これらは、容量が大きくなるとノイズも増大します。図4 は、近端、遠端の容量と遠端のクロストークの振幅を示します。容量と ξ23 にほぼ比例していることが分かります。図7、図8 に容量の有無によるクロストークの波形の違いを示します。
まとめ
以上の解析結果を 表2 にまとめて示します。表面層の遠端クロストークの ξ23 との関係や中間層の遠端クロストークの容量との関係は、これまであまり認識されなかったようです。なお、特に遠端クロストークに関しては、線路損失も考慮する必要があるし、信号の立ち上がり時間にも影響を受けるので、実際の回路定数で十分な解析をする必要があると考えます。
| 近 端 | 遠 端 | |||
| 層 | 表面層 | 中間層 | 表面層 | 中間層 |
| ξ23 | ξ23に比例 | 複雑 | 小さい ξ232に比例 |
|
| 線 長 | 無関係 | 線長に比例 | 無関係 | |
| 容 量 | 無関係 | 無関係 | 容量に比例 | |
なお、拙著『ボード設計者のための分布定数回路のすべて』は、この差動クロストークの章を追加して改訂3版として上梓しました。また、筆者のホームページに、差動クロストークの解析ソフトをアップロードしています。ご活用下さい。
差動クロストークの解析ソフトはこちら
脚注1
n個のベクトル、v1、v2、...vn と係数 k1、k2、...kn に対して、k1*v1+k2*v2+...+kn*vn を、ベクトル、v1、v2、...vn の 1次結合、または線型結合といいます。
参考文献
碓井有三 :
(第3版)自費出版, 2016
C.R.Paul : Analysis of Multiconductor Transmission Lines, 2E, Wiley-IEEE Press, 2007
C.R.Paul : Introduction to Electromagnetic Compatibility, Wiley(2006) (ポール,櫻井ほか(訳),(2006) EMC概論, ミマツデータシステム
碓井有三のスペシャリストコラムとは?
基礎の基礎といったレベルから入って、いまさら聞けないようなテーマや初心者向けのテーマ、さらには少し高級なレベルまでを含め、できる限り分かりやすく噛み砕いて述べている連載コラムです。
もしかしたら、他にも気になるテーマがあるかも知れませんよ!
