分布定数

線路にはキャパシタとインダクタが分布していることは、『分布定数回路～何が分布しているのか？』 で述べました。クロストークを定量的に述べるためには互いに結合している線路、すなわち、結合線路のキャパシタとインダクタを理解する必要があります。

負の容量

2本線路の場合には、着目している線路自身のパラメータのほかに、図1 のように、線路間のパラメータが存在します。CM は線路間の容量、LM は相互インダクタンスです。

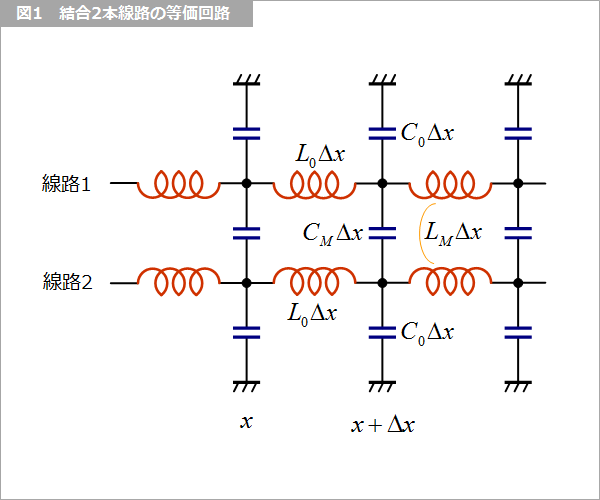
この等価回路の電圧と電流は 図2 の 式(1) および 式(2) ように表されますが、それぞれの式の対称性がよくないので、キャパシタを 式(3) のように置き換えると、対称性のよい式なります。なお、ついでにインダクタについてもキャパシタに合わせて 式(4) のように置き換えます。置き換えた後は 式(5) および 式(6) となって対称性がよくなりました。

図3 はこれらの記号を用いた等価回路です。結合容量が負となっていることに着目下さい。

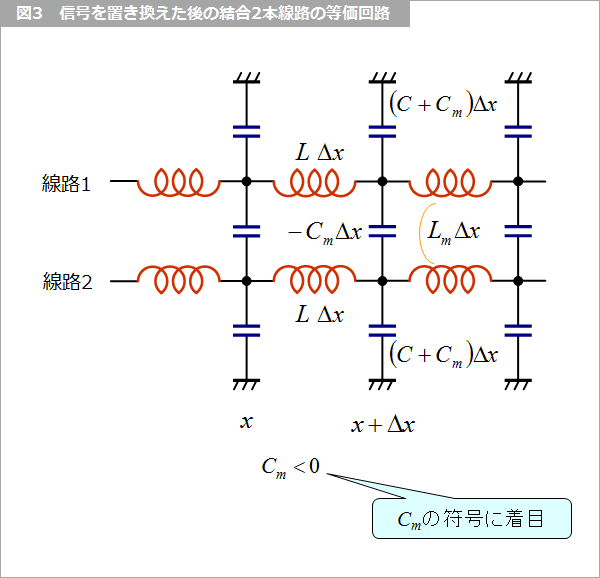
図4 は、方程式をマトリックス表示したもので、キャパシタとインダクタもマトリックスで表します。キャパシタのマトリックスの非対角要素の符号がマイナスになっていることに着目して下さい。

2本だけでなく、3本以上の結合線路の場合にも、線路間の容量は負となります。負の容量といっても、負性抵抗のように電気的に負という意味ではなく、式を扱う上での単なる変換です。したがって、このような変換を行わずに式を解いていくことも可能ですし、そのようにしている例も多く見かけます。ただ、変換した方が簡単で間違いが少ないと思います。

線路定数の求め方

これらのキャパシタやインダクタは簡単な式では求まりません。一般的には、ボードの断面寸法（2次元）を元に、電磁界解析を行います。多くのソフトがありますが、筆者が用いている以下のソフトは、グリーン関数を用いています。

断面寸法からパラメータを得る GreenExpress V2
※ Windward 社が閉店したため、解析ツール GreenExpress V2 を入手することができません。

図5 に示すように、ボードの断面寸法から特性インピーダンスを求める近似式が用いられることがあります。この近似式の発表当時は、近似が成立する範囲の条件が付いていたと思いますが、近似式だけが一人歩きしている可能性があります。文献が手元にないので確認出来ませんが、1960年代のマイクロ波の文献だったと記憶しています。

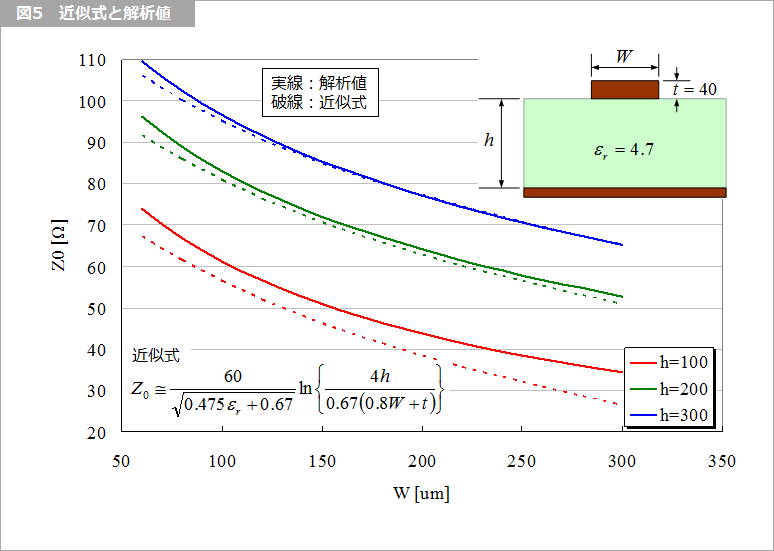
結合線路の伝搬定数

図6 に示すように、これらの L と C の定数を用いて、特性インピーダンスと伝搬遅延とを表すことが出来ます。2本線路では特性インピーダンスと伝搬遅延は 2組存在し、それぞれ、コモン（common）モードとディファレンシャル（differential）モードと呼びます。（脚注1）

それぞれのモードを頭文字の C と D をつけて表すと、特性インピーダンスと伝搬遅延は、図6 に示すようになります。

前述のように、Cm は負なので、ZC と ZD との関係は、常に ZC＞ZD です。遅延時間は、ボードの中間層（または内層）では tdC=tdD ですが、表面層（または外層）では、tdC＞tdD です。

なお、『差動クロストークの厳密解』では、表1 に 4本線路の例を記載しています。

脚注1
コモンモードのことを偶モードあるいはイーブン（even）モードと呼ぶこともあり、ディファレンシャルモードは同様に、奇モードあるいはオッド（odd）モードと呼ぶこともあります。