2本線路の特性インピーダンス

線路に信号が伝搬するとき、隣接して他の第二の線路が存在すると、信号は第一の線路とグラウンド間だけを伝搬するのではなく、第一の線路、第二の線路およびグラウンドを含めた 3者間に伝搬するモードが存在します。隣接した 2本の線路上を伝わる信号には、コモンとディファレンシャルの二つの伝搬モードがあり、互いに特性インピーダンスが異なっています。

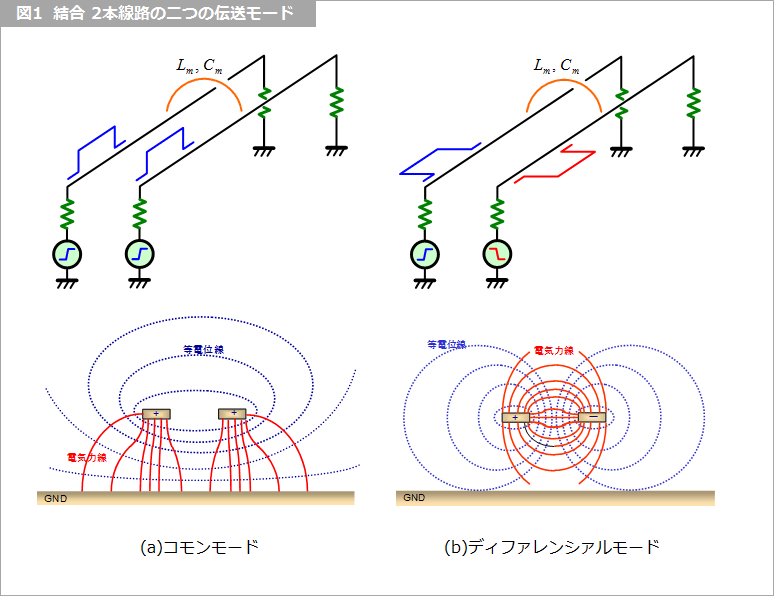
コモンは、図1(a) に示すようなグラウンドに対する伝搬モードです。ディファレンシャルは、図1(b) に示すような線路間の信号の伝搬モードです。この二つのモードの特性インピーダンスや伝搬遅延時間などは、ボードの断面寸法や材料が指定して専用の解析ソフトを用いて求めることが出来ます。（脚注1）

2種類の伝搬モードの重ね合わせ

2種類の伝搬モードとクロストークの関係を簡単に理解するために、ドライバの出力抵抗が R の 2本の互いに等しい結合線路を考えます。

(1) 第一のモード（コモン）

図2(a) に示すように線路 #1、線路 #2 にともに振幅 1/2 のステップ信号を加えます。このときの信号の伝搬モードは、図1(a) に示すコモンのモードなので、このモードの特性インピーダンスを ZC と呼びます。近端の電圧は、同図に示すとおりです。電圧のサフィックスの最初の文字（1 あるいは 2）は、線路の番号を表します。2番目の文字（C あるいは D）はモードを表します。関数の引数は (x,t) で、x は近端を 0、遠端を τ（ギリシャ文字小文字のタウ）としたときの距離、t は波形の立ち上がり時点を 0（ゼロ）としたときの時間です。

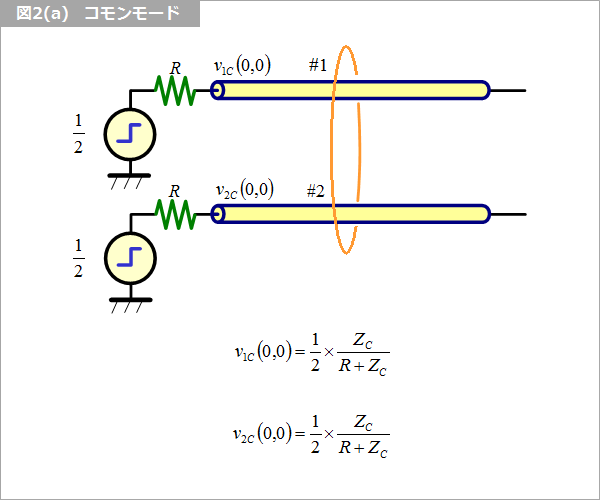
(2) 第二のモード（ディファレンシャル）

図2(b) に示すように、線路 #1 に 1/2、線路 #2 には -1/2 のステップ信号を加えます。このときのモードは 図1(b) に示すディファレンシャルのモードで、特性インピーダンスを ZD と呼びます。電圧は、(1) と同様に図に示すとおりです。

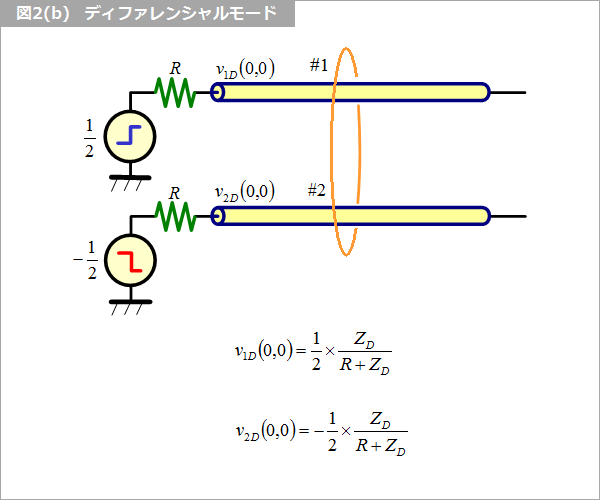
(3) 重ね合わせ（重畳の理）

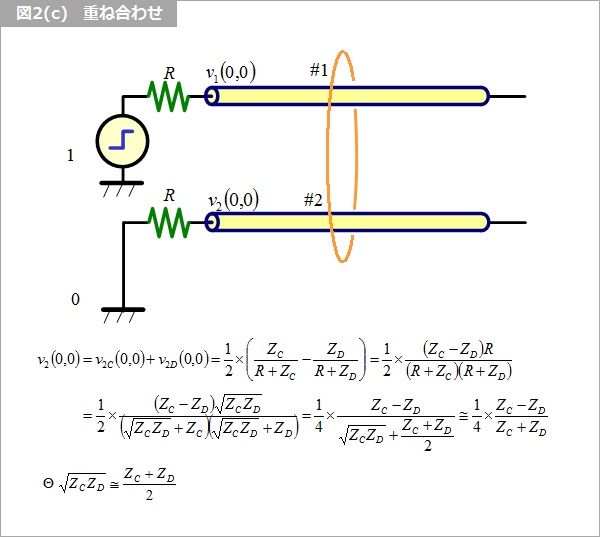
図2(a) と 図2(b) とに重畳の理を適用して重ね合わせると、図2(c) のようになります。線路 1 は 1/2 と 1/2 の和の振幅 1 を加えたことになり、線路 2 は、振幅 1/2 と振幅 -1/2 の和、すなわち、何も加えないことになります。このときの線路 2 の近端の電圧は、図2(c) に示すようになり、ZC と ZD との差があまり大きくないときには、同図に示すように、両者の積の平方根（幾何平均といいます）と通常の平均（算術平均）とはほぼ等しくなります。

特性インピーダンス

コモンとディファレンシャルそれぞれの特性インピーダンス ZC および ZD は、『差動インピーダンスとは？』で述べたように、

ZC = √(1+ξ)/(1-ξ)×Z0、ZD = √(1-ξ)/(1+ξ)×Z0

と表されます。

基礎クロストーク係数

図2(c) の v2(0,0) に現れる、(ZC-ZD)/(ZC+ZD) はクロストークの式によく出てくるので、これを基礎クロストーク係数 ξ、または単にクロストーク係数といいます。ξ は、ギリシャ文字で、クシー、クサイ、グザイなどと発音し、アルファベットの x に相当します。ξ を変形すると、図3 のようになり、インダクティブな結合、Lm/L とキャパシティブな結合 Cm/C の絶対値の平均であることが分かります。

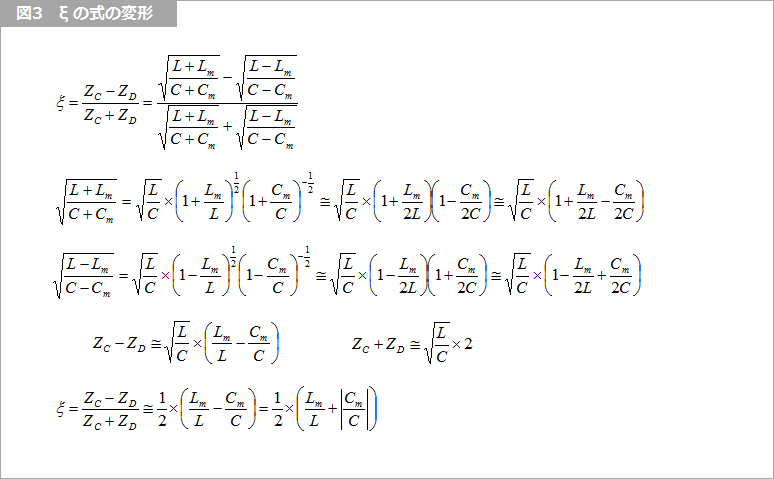
クロストーク係数の前に、なぜ「基礎」がついているか、その他の定義との関係などについては、別の機会に述べます。

脚注1
例えば、GreenExpressV2
※ Windward 社が閉店したため、解析ツール GreenExpress V2 を入手することができません。

参考文献
J. A. DeFalco, "Reflection and crosstalk in logic circuit interconnections," in IEEE Spectrum, vol. 7, no. 7, pp. 44-50, July 1970.
碓井有三 :

ボード設計者のための分布定数回路のすべて(第3版)

　自費出版 , pp. 69-74, 79-81, 2016