分布定数回路の周波数応答

図1に、分布定数回路の周波数応答の式を示します。

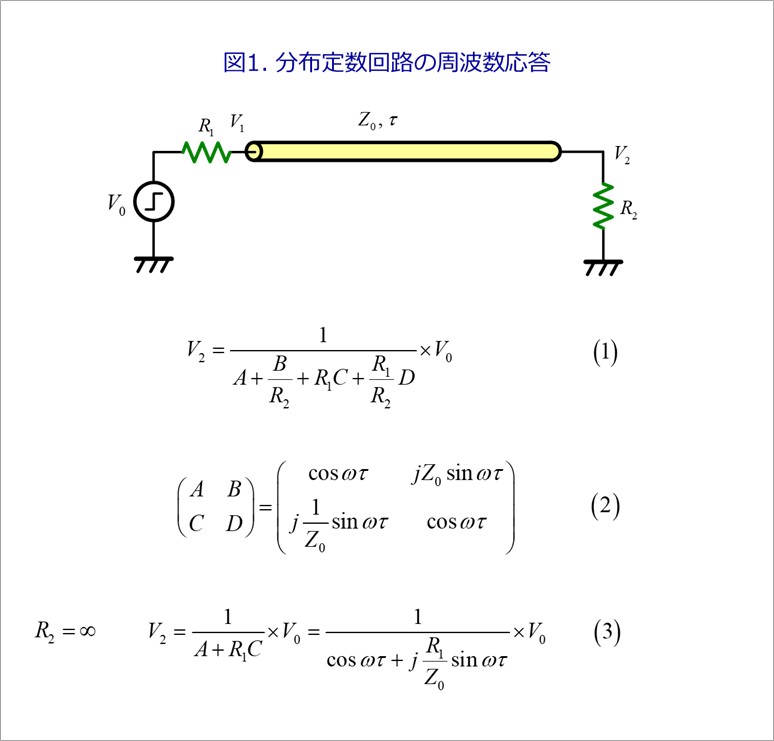
遠端の電圧V2を求めるには、縦続行列を使うのが便利です。
同図の式(1)が縦続行列を用いた遠端の電圧V2です。
縦続行列を式(2)に示します。参考文献(1)
通常のCMOSは、遠端が開放なので、R2=∞で、これを式(2)に代入すると、式(3)のように簡単な式になります。

図2の信号源V0の最も簡単なものは、図2に示す台形波です。

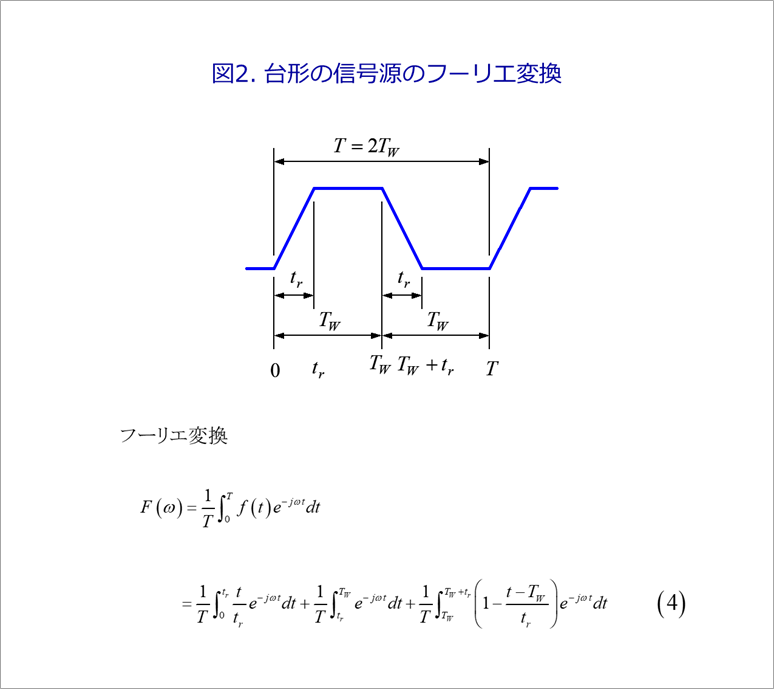
この台形波の周波数関数は、オーソドックスには、図2の式(4)のように、立ち上がり部、平坦部、立ち下がり部に分けてフーリエ変換することによって求めます。
右辺の第1項と第3項は、部分積分を用いて計算しますが、思ったより煩雑で、たぶんA4の計算用紙2枚程度の計算量となり、ちょっと煩雑です。

実は、ラプラス変換とフーリエ変換とは積分の形が似ています。ラプラス変換は、その都度積分をするのではなく、公式を用いるので、比較的簡単に計算できます。ラプラス変換した後、s=jωとおいて、積分区間で割れば、フーリエ変換が得られます。

フーリエ変換とラプラス変換とは、本質的には違います。
数学的に解説すると、いろいろ面倒なことが出てきますが、回路屋という立場だと、両者は親戚みたいなものだと言っても問題ないと思います。
数学の専門家の方からは叱られそうですが。

図2の台形波のラプラス変換は、図3の式(5)に示すように、1行で表されるほど簡単に求められます。

この式(5)は、ランプ波形(1/s^2)の時間遅れの加減算です。
ラプラス変換の結果に、式(6)のように、s=jωとおいて、積分区間Tで割ると簡単に周波数関数を求めることができます。当然、式(4)と式(6)とは同じです。

分布定数回路の時間(ステップ)応答

図1のV0を、図3のF(ω)とすると、遠端の電圧V2は、図4の式(7)となります。

式(7)はωの関数であり、フーリエ逆変換することによって、時間関数v2(t)が得られます。

以上は、周波数解析して、フーリエ逆変換することによって時間応答を求めるものです。次に、

図5の式(8)は、反射の繰り返しにより遠端の電圧を求める基本式です。参考文献(2)
CMOS伝送の場合は、R2=∞なので、r2=1となり、式(9)のように、やや簡単になります。

図6は、図5の式(9)のv0(t)が振幅1のステップ波形の場合を示します。

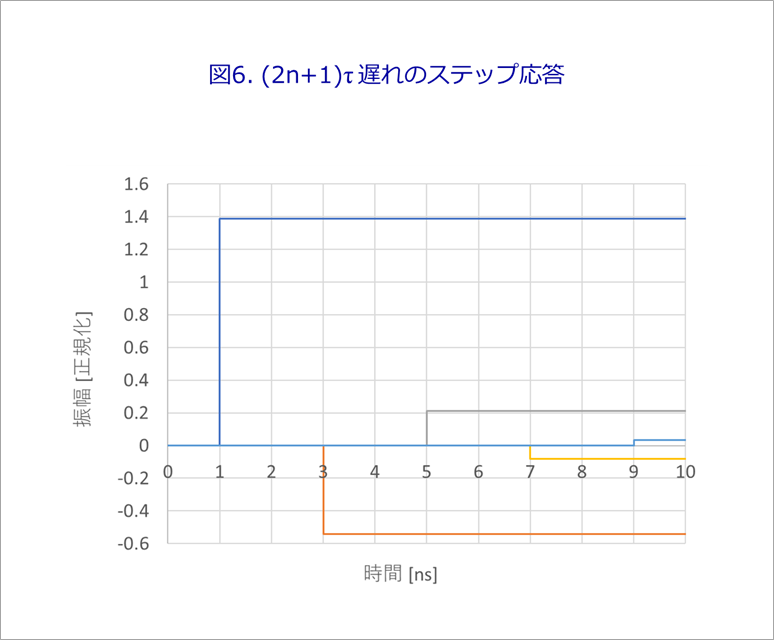
R1=22Ω、Z0=50Ωとして、線路の遅延時間τを1nsとします。
τ(1ns)遅れて、最初の2Z0/(R1+Z0)の振幅が現れ、さらに2τ、すなわち、3τ遅れて近端の反射係数r1(=-0.389)を掛けた振幅、次に5τ、7τ、...(2n+1)τとそれぞれτの奇数倍遅れた波形となります。

図7は、図6のτの奇数倍遅れた波形を加え合わせたものです。これが遠端の電圧V2となります。

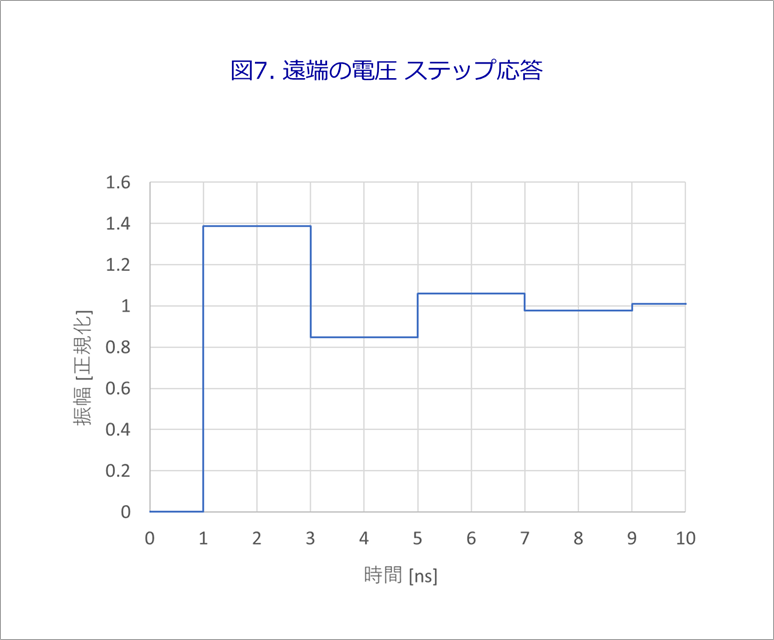
以上のステップ応答は、反射の仕組みを理解するのに役立ちますが、実際の波形は傾きを持ちます。

ランプ波形による重ね合わせ

ステップ応答ではなくて、有限の傾きを持った波形(ランプ波形)で同様に解析します。

図8は、図6と同様のランプ波形です。

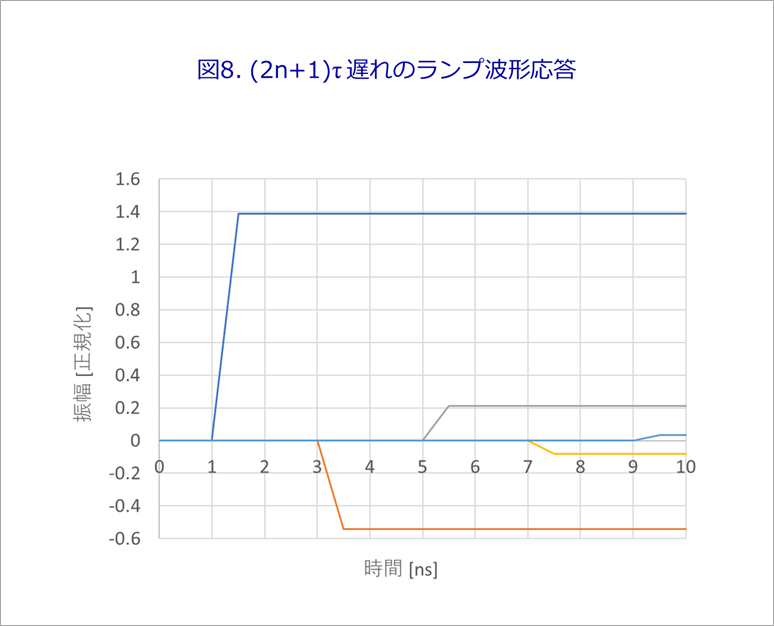
図9は、図7と同様に、図8のτの奇数倍遅れの波形を加え合わせたものです。

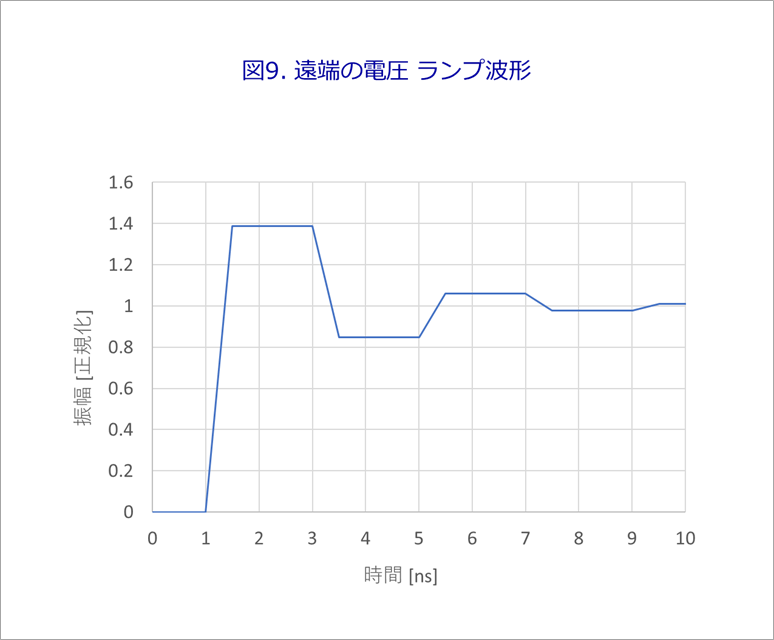
少し実際の波形に近づきました。

ステップ波形+ベッセルフィルターの波形

次に、本稿の目的である、ステップ波形をベッセルフィルターに通して得られた波形を信号源とします。

以下を参照ください。
ベッセルフィルターと他のフィルターの違い その2

この稿の図11は、ベッセルフィルターにステップ波形をを通したときの波形です。
同図は7次低域通過型フィルターLPF(LPF : Low-Pass Filter)ですが、次数が3でもほぼ滑らかな立ち上がり部が得られます。
フィルターの次数の違いによる立ち上がり部の波形については、同じく図12(a)～(c)を参照ください。

これらは、遮断(カット・オフ)周波数fcを1に正規化しています。
図10の式(10)は3次ベッセルフィルターの伝達関数F(s)です。

このフィルターに、ステップ波形を加えたときの、0%-100%の立ち上がり時間trとfcとの積は、3次ベッセルLPFの場合、式(11)に示すように、fc×tr=0.3897となるので、tr=0.5nsとするなら、fc=0.3897/0.5ns=779MHzとなり、3次ベッセルの場合は、f0=fc/1.756=444MHzとなります。

LPFを通すと、遅延が生じます。
ベッセルフィルターの遅延は、ほぼ群遅延で、1/ω0です。
3次ベッセルの場合、1/ω0は、式(12)に示すように、0.385nsです。

7次ベッセルの伝達関数は式(13)です。
3次と同様に、fcとf0を式(14)に示します。
群遅延は、式(15)に示すように1/ω0=0.216nsとなります。

これらの遅延は、ベッセルを通した際に生じるので、時刻 t=0で立ち上がるようにするには、この遅延分を考慮する必要があります。

時間応答(ラプラス逆変換)

ベッセルLPFのステップ応答は、伝達関数にステップ波形の1/sを掛けてラプスラ逆変換をします。

図11の式(16)は、ベッセル3次LPFにステップ波形を加えたものです。

同式の右辺は、分母を1次式と2次式の積に因数分解したもので、この右辺の分子の因子の係数は、式(17)のようになります。

式(16)のラプラス逆変換を求めるには、式(18)のように部分分数展開します。
同式の右辺の第3項の分子は、単に、Cs+Dでもよいのですが、ラプラス逆変換しやすいように同式のようにCとDに係数を掛けておきます。参考文献(3)

式(18)の未知の係数、A～Dは、同式の分母を払って、sに関する恒等式に変換して、sのべき乗ごとの係数を右辺と左辺で比較します。
右辺は、定数項のみなので、左辺のsのべき乗の係数は全て0(ゼロ)となります。
式(20)は、これらを連立方程式としたもので、これを解いて、A～Dを求め、ラプラス変換します。

図12の式(21)、(22)は、式(18)の右辺第3項のラプラス逆変換で、コサインとサインに変換されます。いずれも指数の減衰項を含みます。参考文献(3)

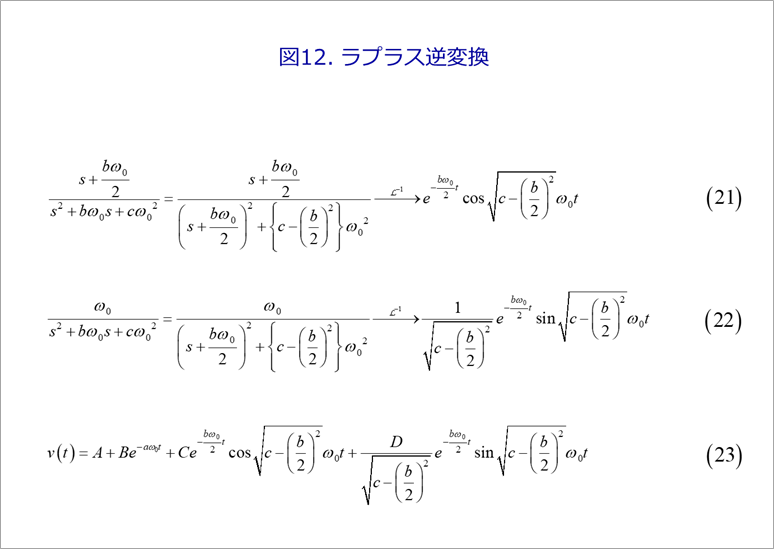
式(23)は、ラプラス逆変換した結果です。

図13(a)は、式(23)の立ち上がり部を示したものです。

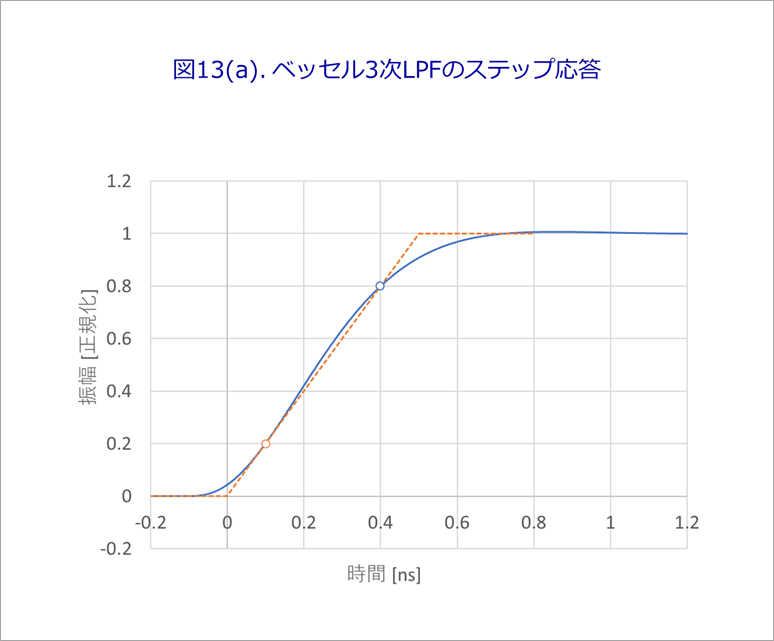
立ち上がりの20%と80%の点を直線で結んだランプ波形を同時に示します。
これらは、3次ベッセルLPFの場合ですが、例えば、7次LPFに関しても、やや煩雑ですが、同様に求めることができます。
式(16)に対応する7次は、分母が1次と2次×3に因数分解できます。
式(20)と同様に、連立方程式を立てて、未知の係数を求めます。
その結果を図13(b)に示します。3次に比べて、20%-80%の部分が直線に近いことが分かります。

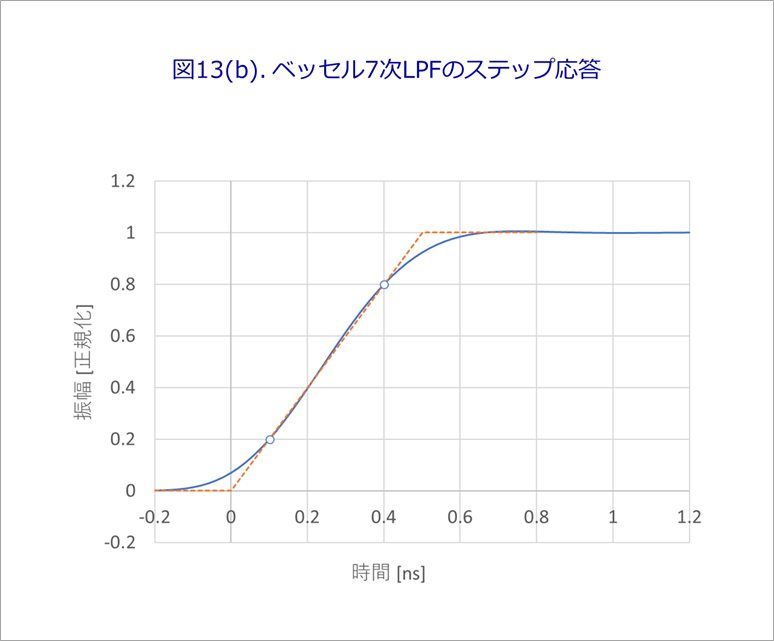
図13(b)の波形を元に、反射波形を計算して、図6や図8と同様に、図14のように、各タイミングの波形を求めます。

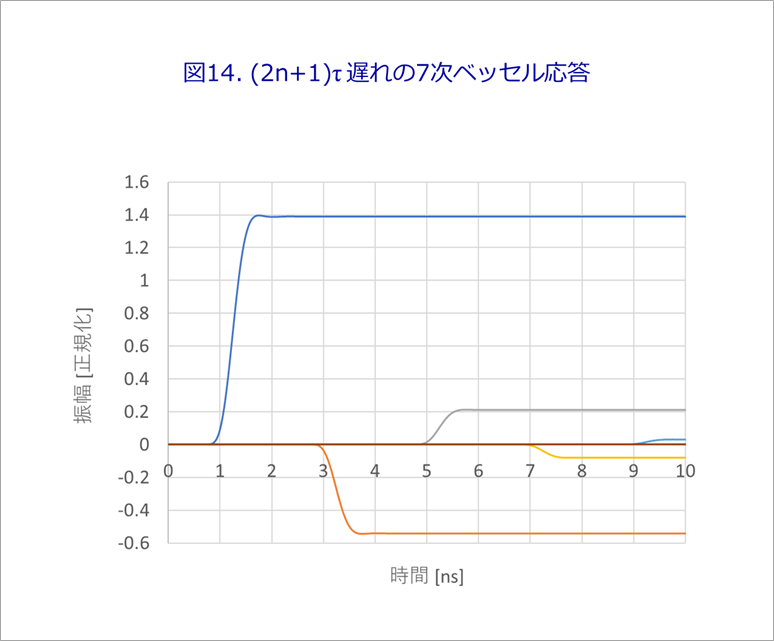
図15は、図14の波形を時間軸で重ねたもので、実際の反射波形に近い波形を得ることができました。

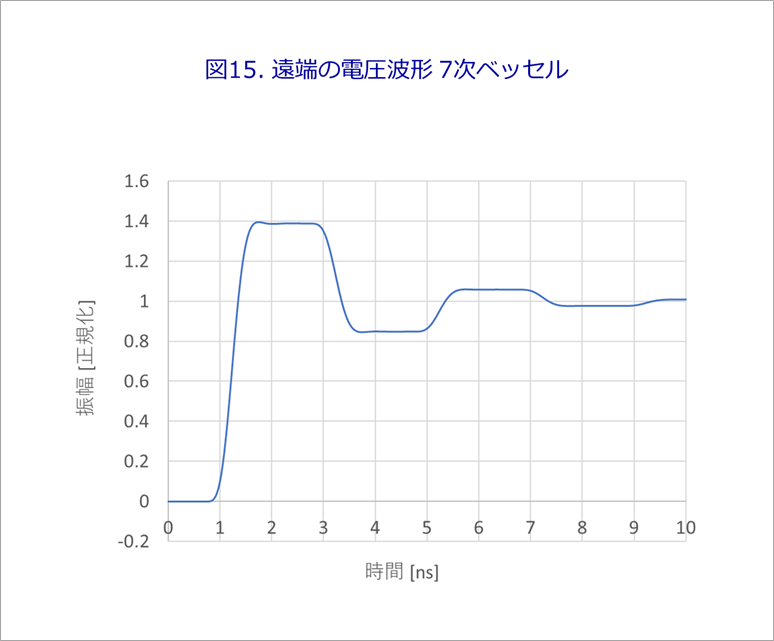
これは、IBISのWaveformデータを用いた解析手法と同様です。
以下を参照ください。

IBIS モデルを用いた反射の解析～その2

参考文献
(1)碓井有三 : "ボード設計者のための分布定数回路のすべて 第3版"自費出版、2016 (http://radioy.a.la9.jp/book/book.htm)、pp.156-158

(2)同書、pp.20-43

(3)同書、p.232