縦続行列

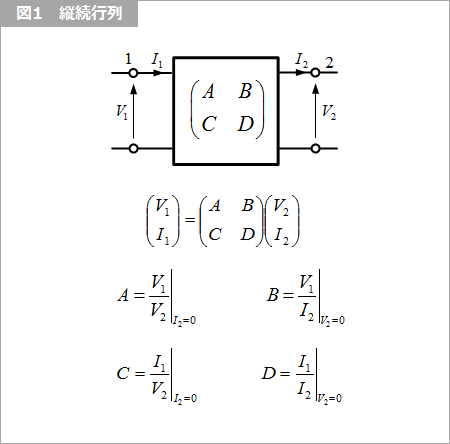
図1 は縦続行列の電圧と電流との関係です。A、B、C、D は 図1 に示す式で求めることができます。

右行波と左行波

準備段階として、分布定数線路の電圧と電流は、

電圧=右行波+左行波
電流=右行波-左行波

で表されます。右行波は、ラプラス変換の公式

f(t-a) ⇔ exp(-as)F(s)

を用います。f(t-a) は、時刻 t=a のときに f(0) すなわち原点になるということは、a だけ遅れることを意味します。すなわち、右に時間 a だけ進んだ場所の波を表します。左行波は、逆に、

f(t+a) ⇔ exp(as)F(s)

を用います。

電圧と電流の式

信号（波）の速度を u とすると、原点（近端）からの距離 x までの遅延時間は、x/u です。x における電圧は、

V=A1*exp(-sx/u)+A2*exp(sx/u)

電流は、

I=(A1*exp(-sx/u)-A2*exp(sx/u)}/Z0

となります。A1、A2 は、近端と遠端の境界条件により決まる定数です。ここで、s=jω とおくと周波数関数になり、FFT が使えます。

線路の遅延時間を τ とすると、近端と遠端の電圧・電流は、

V1=A1+A2V2=A1*exp(-jωτ)+A2*exp(jωτ)
I1=(A1-A2)/Z0
I2=A1*exp(-jωτ)/Z0-A2*exp(jωτ)/Z0

と表されます。

縦続行列の A と C

A と C は、I2=0 なので、端子2（遠端）を開放します。

I2=A1*exp(-jωτ)/Z0-A2*exp(jωτ)/Z0=0

なので、

A1*exp(-jωτ)=A2*exp(jωτ)

すなわち、

A2=A1*exp(-2jωτ)

したがって、

V2=A1*exp(-jωτ)+A2*exp(jωτ)=2A1*exp(-jωτ)

近端の電圧は、

V1=A1+A2={1+exp(-2jωτ)}A1

なので、

A=V1/V2={1+exp(-2jωτ)}/{2A1*exp(-jωτ)}
　={exp(jωτ)+exp(-jωτ)}/2

となります。ここで、オイラーの公式

exp(jθ)=cos(θ)+jsin(θ)

を用いて、

A=cos(ωτ)

となります。

同様の条件 I2=0 で C を求めると、

I1=(A1-A2)/Z0=A1/Z0{1-exp(-2jωτ)}
V2=2A1*exp(-jωτ)

したがって、

C=I1/V2=A1/Z0{1-exp(-2jωτ)}/{2A1*exp(-jωτ)}
　={exp(jωτ)-exp(-jωτ)}/(2Z0)

同様にオイラーの公式を用いて、

C=jsin(ωτ)/Z0

となります。

縦続行列の B と D

次に、B と D を求めるには、V2=0 なので、

V2=A1*exp(-jωτ)+A2*exp(jωτ)=0

なので、

A2=-A1*exp(-2jωτ)

したがって、

V1=A1+A2={1-exp(-2jωτ)}A1
I2=A1*exp(-jωτ)/Z0-A2*exp(jωτ)/Z0
　=2A1*exp(-jωτ)/Z0

したがって、

B=V1/I2={exp(jωτ)-exp(-jωτ)}*Z0/2

オイラーの公式を用いて、

B=jZ0sinωτ

となります。

次に D を求めます。

I1=(A1-A2)/Z0=A1/Z0{1+exp(-2jωτ)}
D=I1/I2={1+exp(-2jωτ)}/{2*exp(-jωτ)}

オイラーの公式を用いて、

D=cos(ωτ)

となります。

分布定数線路の伝達関数

図2 に以上により求めた分布定数線路の縦続行列を示します。縦続行列が求まると、『縦続行列』 図3 伝達関数 により伝達関数を求めることができます。

簡単のために、R1=R、R2=∞とすると、

F(ω)=1/(A+RC)
　=1/(cosωτ+jR/Z0sinωτ)

となります。

FFTによる波形解析

パルス波形の iFFT（逆変換）は、『エクセルによる FFT』で述べました。このときのパルス波形に、上記 F(ω) をかけてフーリエ逆変換をします。エクセルの複素数の掛け算は、improduct 関数を用います。

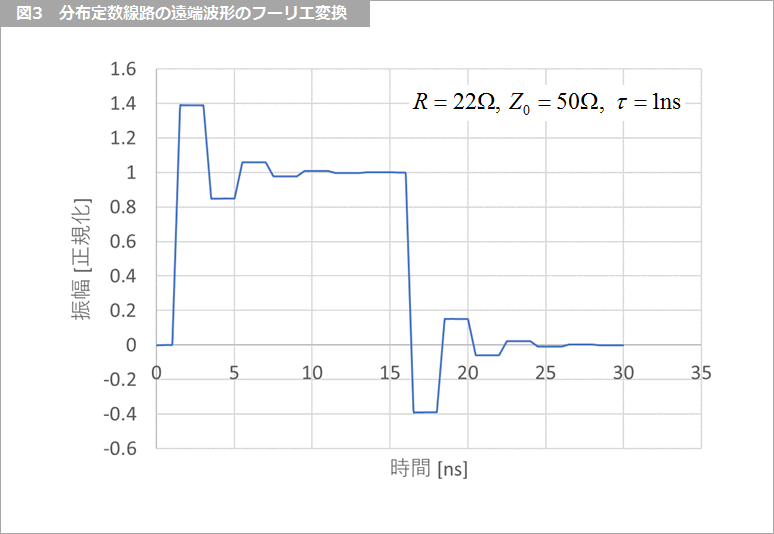
図3 に、1024点の解析結果を示します。パルス幅が 15ns、周期が 30ns ですが、周期が短いと、反射の途中で次のパルスがくるので、正しい単発の応答を求めることができません。逆に、実際の周期が短い場合には、その周期の応答を求めることができます。使い分けてください。