アナログ信号を標本化する場合に、標本化周波数の半分より高い周波数を除去する必要があります。
この目的で用いるのはベッセルフィルターです。
ベッセルフィルターについて、他のフィルターの形式と比較して、2回に分けて解説します。
図の番号は、その1、その2で通しでつけています。

以下を参照ください。

FFTにおける折り返しノイズ(エイリアス)

この用途には、ベッセル(Bessel)の低域通過型フィルター(LPF : Low-Pass Filter)を用います。

低域通過型フィルターとは、設定した周波数以下を通過させて、それ以上の周波数を遮断します。この設定した周波数を、遮断(カット・オフ)周波数、通過させる周波数域を通過域、遮断する周波数域を遮断域といいます。

理想的には、通過域は減衰ゼロ、遮断域は無限大の減衰ですが、実際には、境界の周波数以上は、例えば、周波数が倍になると12dB(デシベル)とか24dBなどの傾きで減衰します。この減衰特性をロールオフ(roll-off)特性といいます。
このロールオフ特性の値は、フィルターの段数1段あたり-6dBとなります。[脚注1]
周波数が倍になることを、オクターブ(またはオクターヴ)というので、-6dB/octのように表記します。6段なら-36dB/octとなります。オクターブは、音楽の8度の音程(例えば下の「ド」から上の「ド」)としてもよく使われます。octは、ラテン語のocto(8)からきています。
周波数の2倍ではなく、10倍で考えると、-6dB/octは、-20dB/decとなります。
decは、decadeで10を表します。

フィルターは、低域通過型の他に、高域通過型(HPF : High-Pass Filter)、帯域通過型(BPF : Band-Pass Filter)、帯域阻止型(BEF : Band-Elimination Filter)に分類できます。
この他に、群遅延特性[脚注2]を制御する、全域通過型(APF : All-Pass Filter)もあります。

フィルターの特性で分類すると、ベッセルフィルターの他に、バターワース(Butterworth)フィルターやチェビシェフ(Chebyshev)フィルターなどがあります。

それぞれの特性の違いは、通過域の平坦性と減衰特性および群遅延で、その特徴にあわせた用途があります。
通過域の平坦性は、ベッセルが最も平坦で、チェビシェフは通過域にリプルが存在します。
減衰特性は、チェビシェフが最も急峻で、ベッセルが最も緩やかです。
群遅延は、ベッセルが最も平坦で、チェビシェフは最も乱れます。

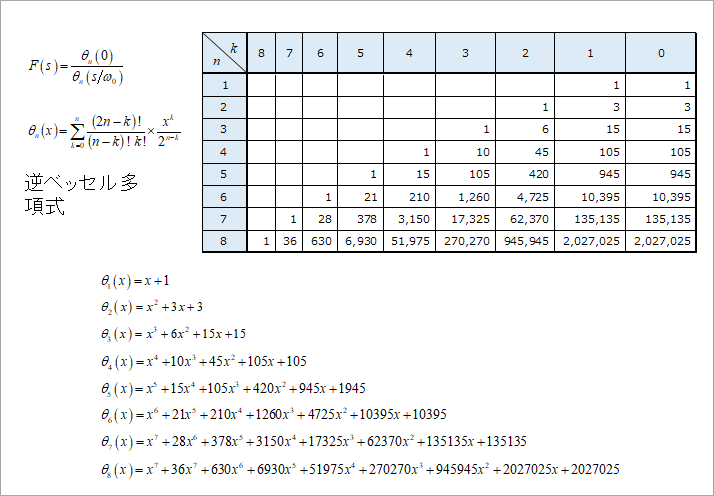
ベッセルフィルターの伝達関数を、図1のF(s)に示します。θnは逆ベッセル多項式で、n=1から8までを図1に示します。同図の表は、この多項式のそれぞれの係数を整理したものです。

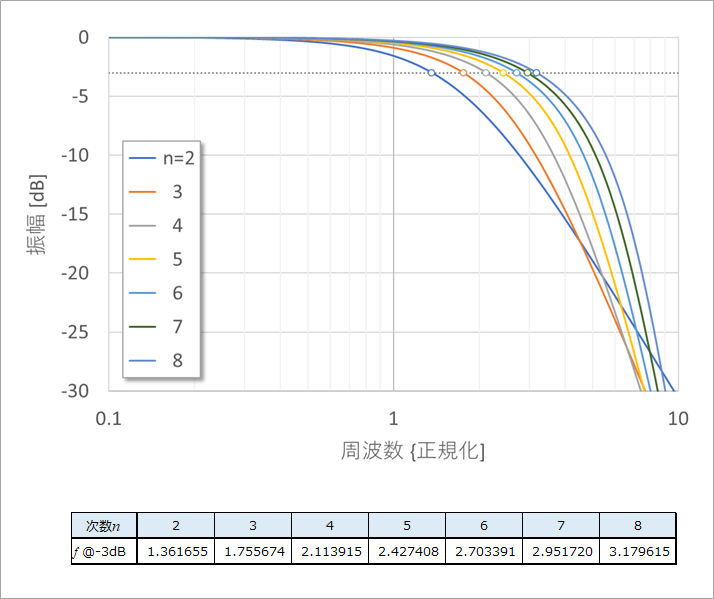
図1のF(s)のまま周波数特性を求めると、図2に示すように、-3dBの点が、同図の表に示すように、正規化周波数になりません。例えば、n=3のオレンジ色の特性では、-3dBの点(正規化周波数)は、1.76です。
したがって、周波数をこの表の値で割る必要があります。

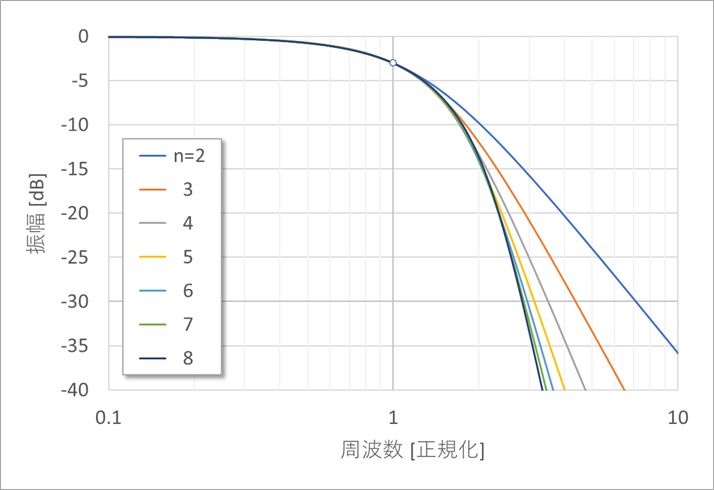
図3は、周波数を図2の表の値で割った場合の周波数特性です。
以下、ベッセルフィルターの特性は、この図を基本とします。

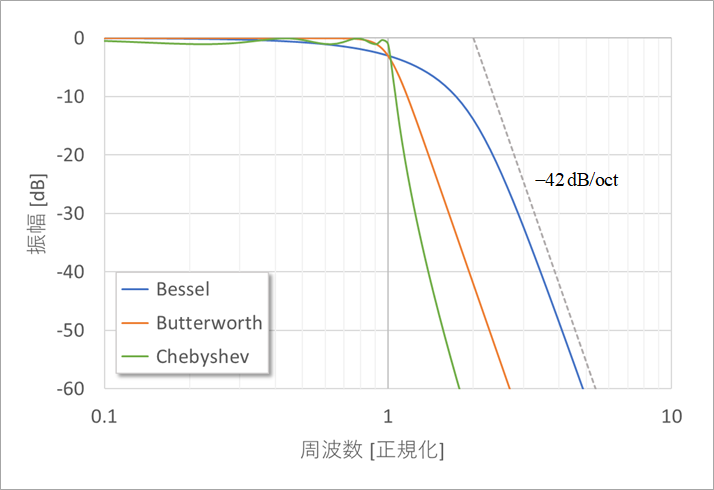
図4は、3種類のフィルターの減衰特性を比較して示したものです。フィルターの次数は7で、ロールオフの特性は、-42dB/octです。遮断周波数は1に正規化しています。この場合のチェビシェフのリプルは1dBとしています。

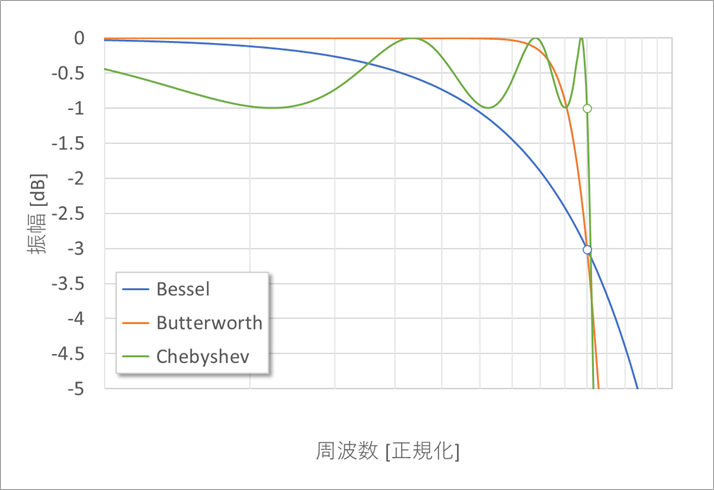
図5は、図4の通過域から遮断周波数付近までを拡大して示したものです。
上で述べた、各フィルターの特徴がよく現れています。
ベッセルとバターワースの遮断周波数の減衰量は-3dB[脚注3]です。
チェビシェフは、リプルの値に負号をつけたもので、この場合は-1dBです。[脚注4]

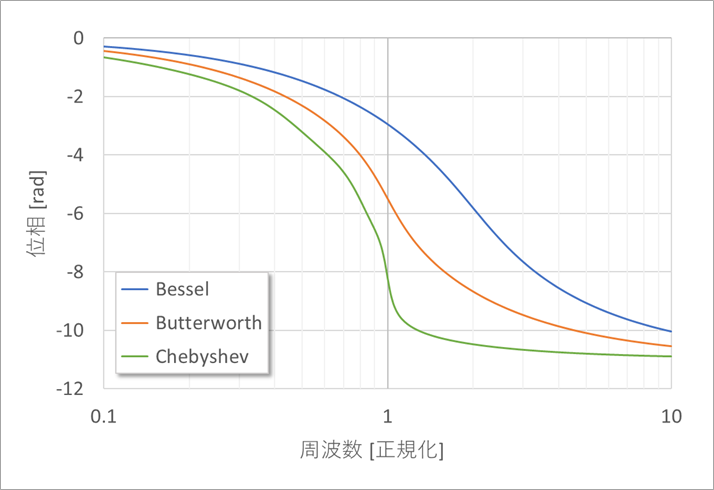
図6は各フィルターの位相特性です。ベッセルは緩やかに、チェビシェフは急峻に変化します。

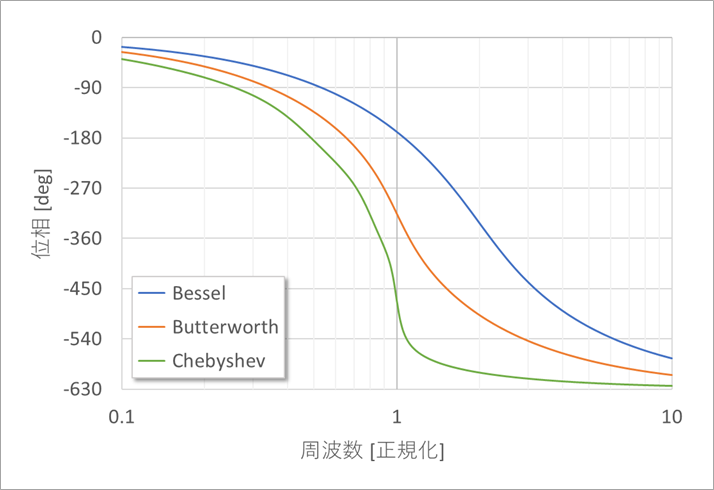
図7は位相を度で表したものです。
次数1ごとに最大-90度変化するので、7次の場合、-630度まで変化します。

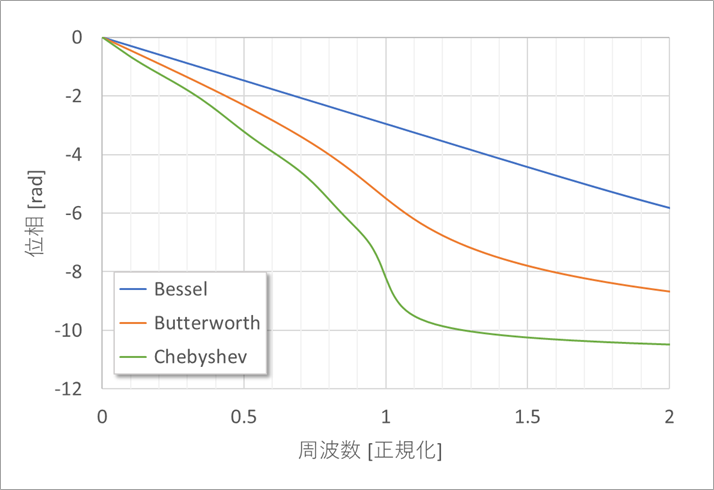
周波数特性は、通常、横軸は周波数を対数で表します。
ここで、位相の直線性を見るために、図8のように周波数軸を線形で表すと、ベッセルは周波数に対して直線的に変化していることが分かります。

本コラムは、シグナルインテグリティーを中心に述べています。
扱う信号はパルス波形が中心です。
バルス波形を忠実に伝送するには、振幅特性はできるだけ平坦に高い周波数まで伸びて、位相はできるだけ周波数に対して線形である必要があります。
この波形歪みを評価するために群遅延という尺度があます。
脚注2に述べたように、位相の角周波数による微分で表します。

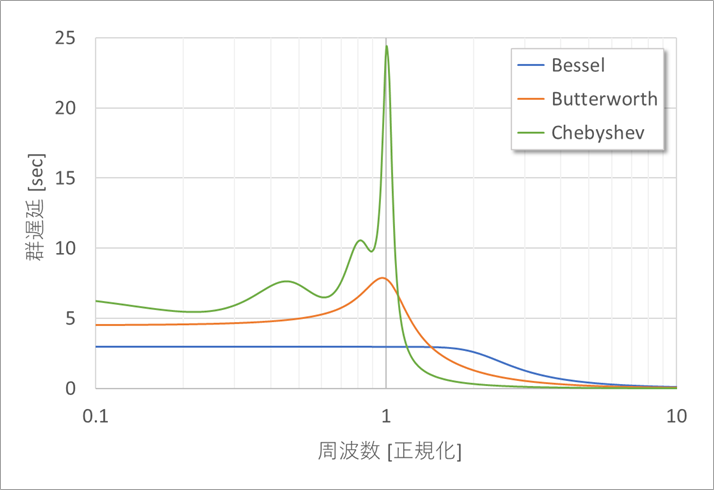
図9に群遅延特性を表します。
ベッセル以外のフィルターは、群遅延が大きく変化しますが、ベッセルは通過域ではほぼ一定です。

今回はベッセルフィルターの原理を中心に述べました。
次回は、このフィルターを通したときの信号波形の変化について述べます。

脚注1
-6dBは厳密には、20log(1/2)=-6.0206です。
通常-6dB/octのように表現するときには、6の倍数であることが分かるといいので、通常、小数点以下を用いません。

脚注2
群遅延(GD : Group Delay)とは、波形の遅延特性です。位相φの直線性を表す指標で、入出力間の位相差を角周波数ωで微分したもので、傾きは負なので式では負号がつきます。すなわち、
GD=-dφ/dω です。

脚注3
-3dBは厳密には、20log(√1/2)=-3.0103です。
これも3dBダウンという用い方をするので、通常、小数点以下を用いません。

脚注4
チェビシェフの遮断周波数の利得については、いろんな定義があるようです。他のフィルターと同様に、-3dBとしたり、フィルターの次数が偶数の場合は、チェビシェフの遮断周波数を-1dBとすると、直流の利得が-1dBになるので、これを避けるため偶数次の場合、遮断周波数の利得を0dBにしたりします。 本稿では、ベッセルを中心に述べるているので、この程度にとどめます。