標本化定理

FFTは、連続波形を離散的な時間でサンプリングします。
標本化するタイミングの周波数を標本化周波数(サンプリング周波数)といいます。

最近(といっても20年以上前から)の高性能のオシロスコープは、リアルタイムで標本化してデジタルデータとして画面に表示したり数値として取り込むことができます。
このようなオシロスコープを、デジタル・オシロスコープといいます。
サンプリングする際に重要なのは、標本化(サンプリング)定理(脚注)です。

対象とする時間関数f(t)の最大の周波数成分fmaxがサンプリング周波数fsの半分以下であるときに完全に復元できるというものです。
すなわち、fmax≦fs/2 です。

ここで、周期T=10nsのときの、N=16のFFTについて考えます。
周期10nsを16の点でサンプリングするので、サンプリング周波数fsは1.6GHzで、fs/2=0.8GHzです。
標本化定理を満たすには、信号周波数が0.8GHz以下であることが条件です。

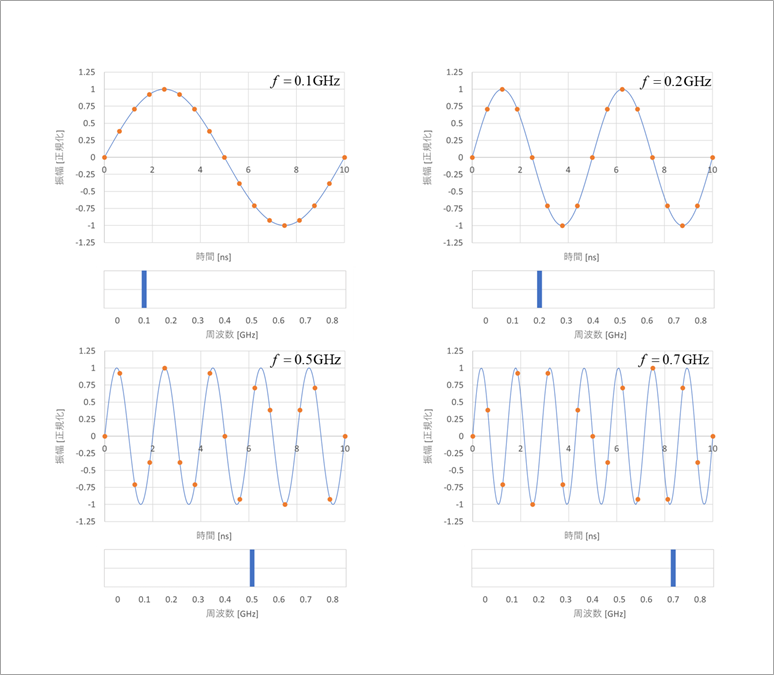
図1は、f≦fs/2 の場合です。
信号周波数が 0.1GH、0.2GHz、0.5GHz、0.7GHz の場合に、信号波形と、オレンジ色のマーカで示すサンプリング点とを示します。
このマーカをフーリエ変換すると、元の周波数のスペクトルが現れます。これを同図の下部に示します。

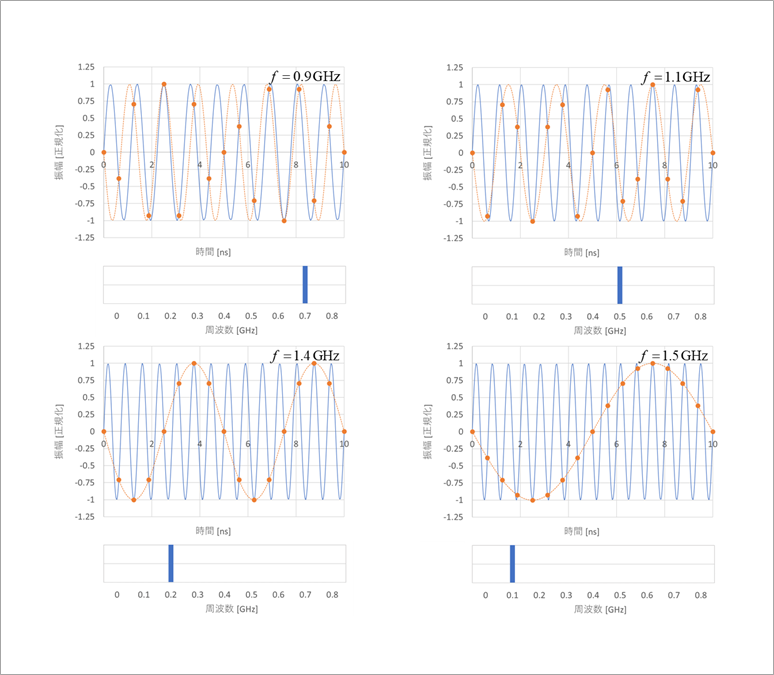
図2は、信号周波数fがfs/2よりも高い場合を同様に示します。
信号周波数が0.9GHzの場合は、fs/2の0.8GHzに関して対称の周波数の0.7GHzが現れます。ただし、波形の極性符号は元信号の逆(マイナス)となります。
1.1GHzなら、fs/2の0.8GHzから上に0.3GHzなので、現れる周波数は、0.8GHzから下に0.3GHz、すなわち0.5GHzとなります。同図の他の周波数に対しても同様です。これは、fs/2に関して折り返した形になるので、折り返し雑音、または、エイリアス(alias)雑音といいます。

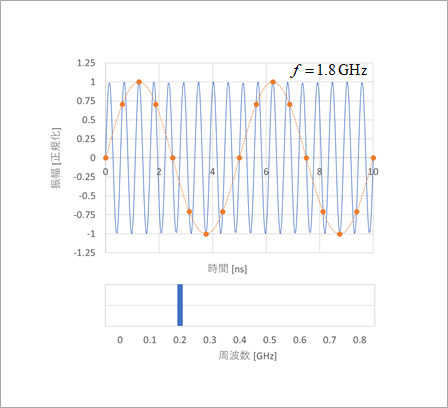
さらに、図3に示すように、fs(1.6GHz)よりも高い1.8GHzの場合、fsに関して折り返します。この場合、fsの1.6GHzに関して折り返すので、1.4GHz、これは、fs/2の0.8GHzに関しての折り返しの0.2GHzとなります。
極性は、マイナスのマイナスなので、元信号と同じ極性です。

したがって、fs/2よりも高い周波数成分を含む信号を、fsで標本化(デジタイズ)すると、高い周波数成分が、低い周波数に化けて(折り返して)現れるので、忠実な波形変換ができません。

エイリアスの例

身近な例として、西部劇の駅馬車の車輪の回転が時々反転しているように見えることがあります。
映画は、1秒間に24コマの映像を連続して動画とします。
すなわち、サンプリング周波数が24Hzなので、その半分の12Hz以上の動きは、12Hzで折り返されることになります。
車輪のスポークが12本の場合、車輪が1秒間に1回転すると、スポークは12Hzの動きをしています。
このとき、車輪があたかも停止しているように見え、それより高い周波数、すなわち、駅馬車が速く進むと、車輪は逆回転しているように見えます。
なぜ逆回転かというと、図2に現れるサイン波の極性がマイナスであることで説明できます。

実際の例

実際の例について考えます。

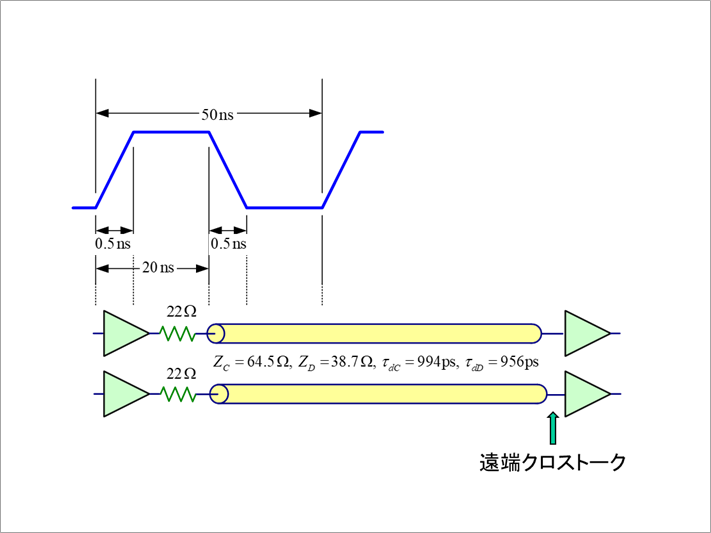
高い周波数成分を含む波形の例として、図4の回路の遠端クロストークの波形を考えます。
この例は、クロストーク係数ξ=0.25、線長15cm程度の表面層を想定しています。

以下も参照ください。

遠端クロストーク

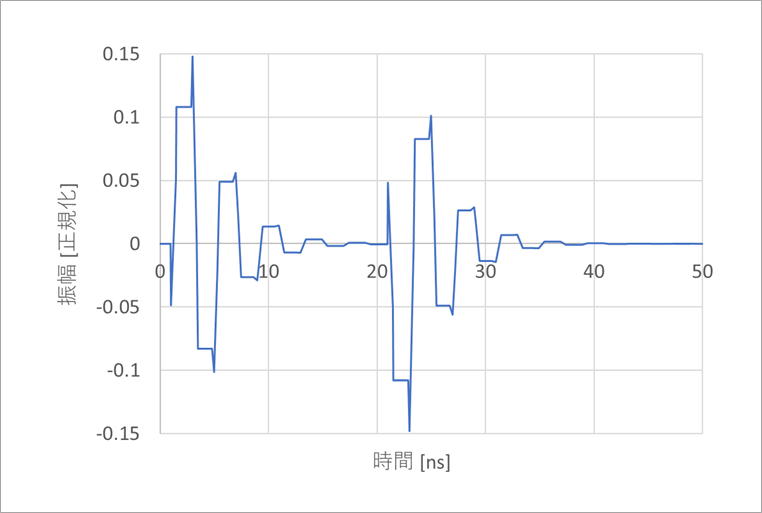
図5は、図4の遠端クロストークの解析結果です。
ひげ状の波形は十分に高い周波数成分を含んでいます。
この計算は、N=16,384点のFFTを用いました。

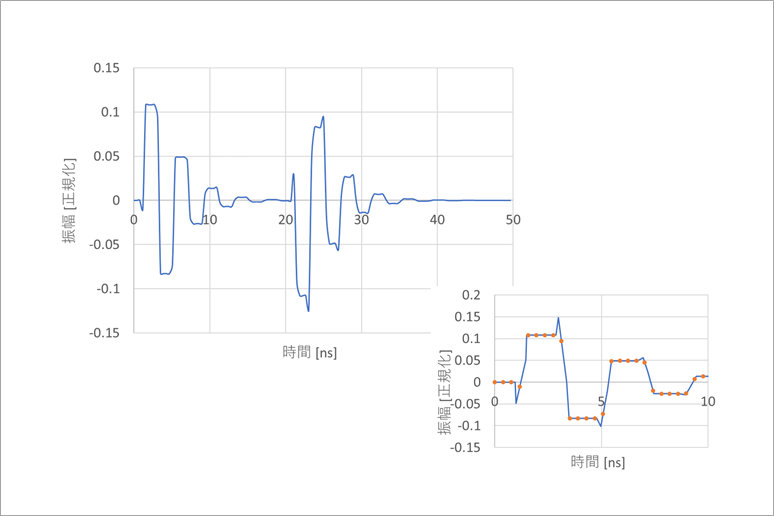
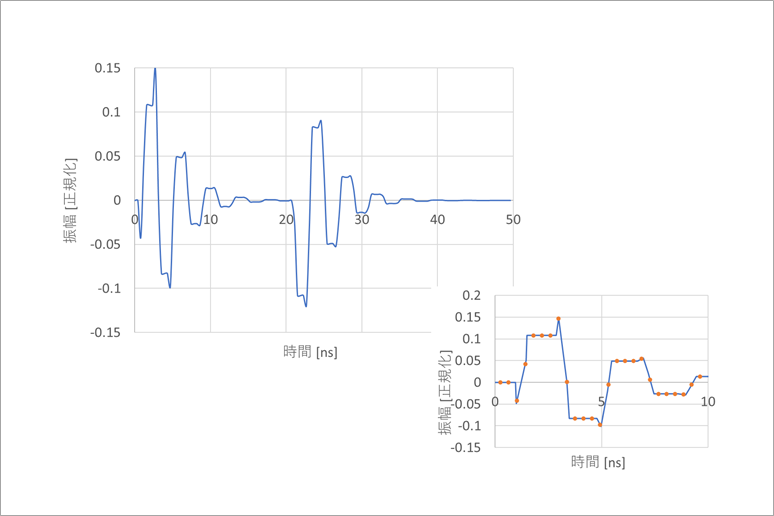
図6は、図5の波形の1周期50nsを128点でサンプリングして、フーリエ逆変換(iFFT)したものです。
サンプリング周波数fsは、2.56GHz(1/50ns×128)です。
図6(a)は、サンプリングが最初のひげ状のピークを外れており、図6(b)は、ちょうどピークにかかるようにサンプリングしたものです。
サンプリング点と波形のピークの点とは一致することも外れることもあるので、128点のFFTはふさわしくないことが分かります。

この原因は、図5の波形が、サンプリング周波数の1/2以上の周波数成分を含んでいるためです。

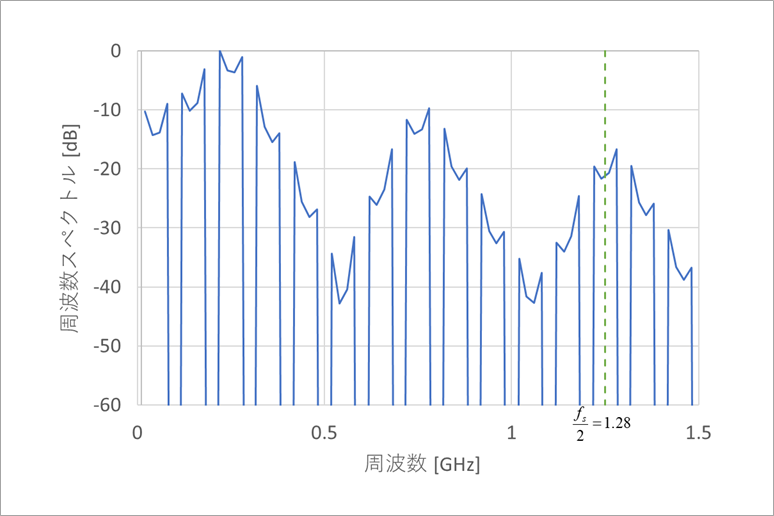
図7は、図5の波形の周波数スペクトルを求めたものです。
通常、周波数特性は横軸(周波数)を対数で表しますが、ここでは折り返しを表すために直線メモリとしています。
fs/2の1.25GHzより高い周波数でも十分なスペクトルが存在しています。

この高い周波数成分を抑制するために、通常、低域通過型フィルタ(LPF : Low Pass Filter)を用います。
このフィルタを、エイリアスを除去するという意味で、アンチ・エイリアス・フィルタと呼びます。

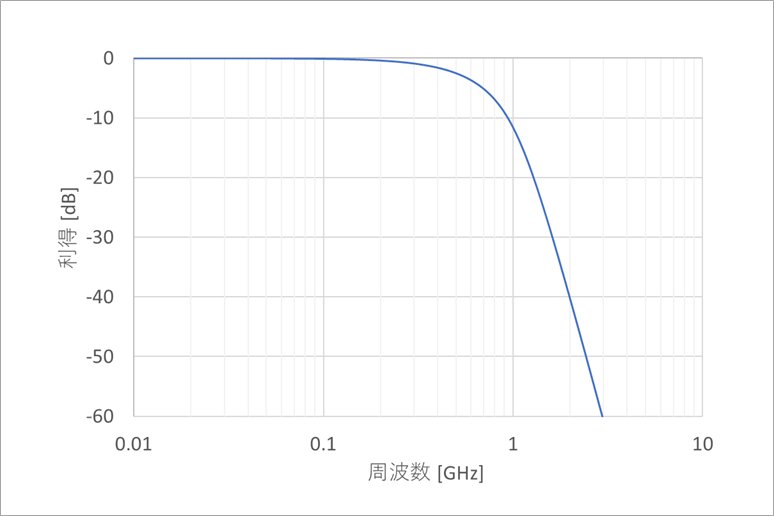
図8は、fs/2(1.28GHz)で20dB減衰するLPFの例です。
フィルタの種類はいろいろありますが、パルス波形には、ベッセル(Bessel)型を用います。
図は、6次のベッセルフィルタです。
ベッセルフィルタの特徴は、減衰特性はなだらかですが、群遅延(Group Delay)が一定なので、波形歪みが小さく抑えられます。
フィルタの特性については、また別の機会に述べることとします。

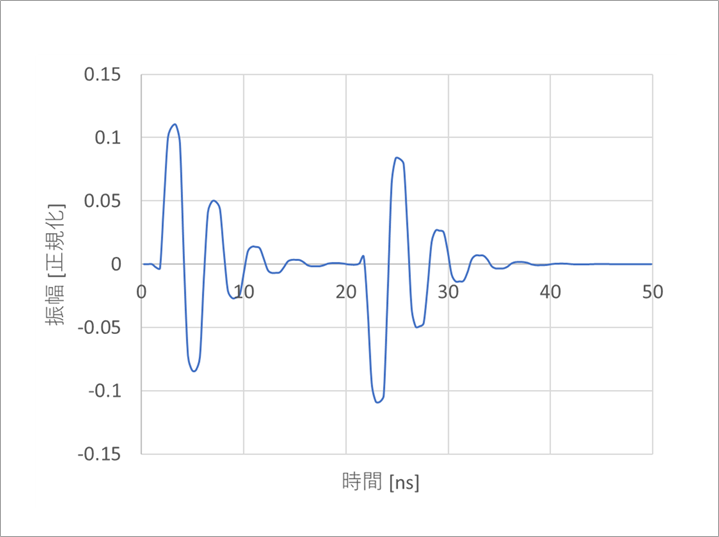
図9は、元の波形(図5)に、図8のアンチ・エイリアス・フィルタを加えて、128点フーリエ逆変換したものです。
当然ながらサンプリング点がずれても波形は変化しません。

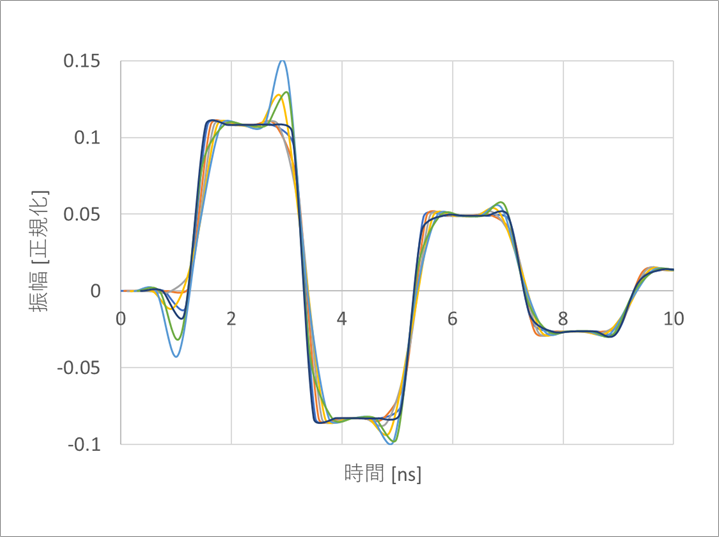
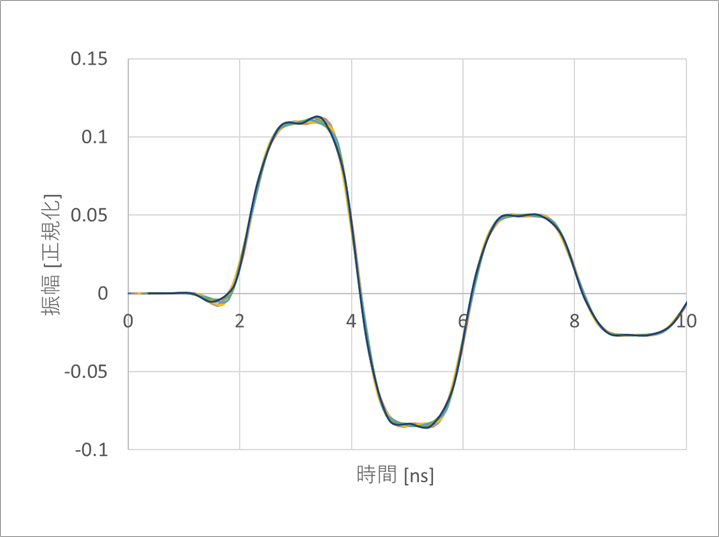
図10(a)は、図6のサンプリング点を変化させた場合の波形を重ねて示したものです。
サンプリング点の変動に大して波形が異なることが分かります。
同図(b)は、アンチ・エイリアス・フィルタを加えた場合について同様に示しました。
サンプリング点が変動しても同一の波形が得られます。
同図(b)は(a)に比べて、立ち上がり点が1ns弱ずれています。これは、アンチ・エイリアス・フィルタを挿入したための遅延です。

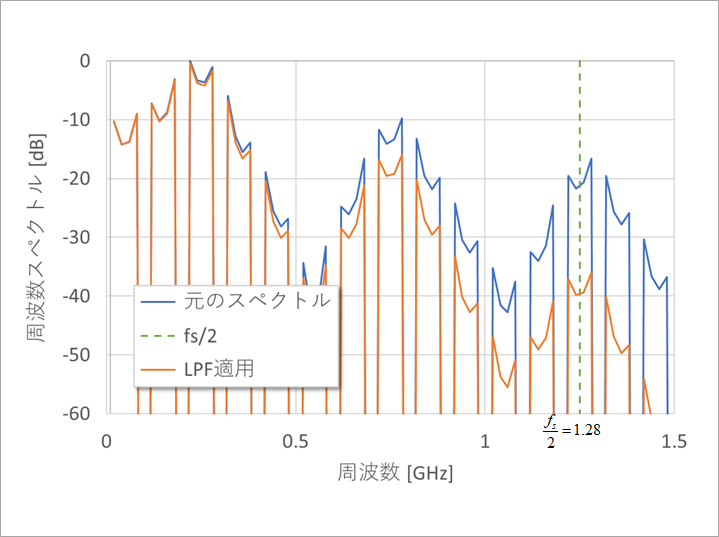
図11は、LPF適用によるスペクトルの変化です。fs/2より高い周波数で十分減衰していることが分かります。

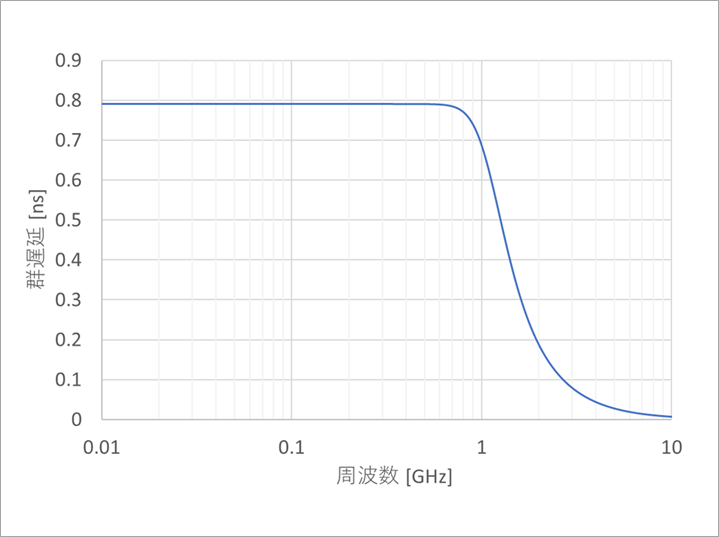
図12は、図8のLPFの群遅延です。1GHz付近まで平坦であることがベッセルフィルタの特徴です。
この遅延特性についても、機会があれば他のフィルタ形式と比較して、述べたいと思います。

脚注

シャノンの標本化定理といいます。
ナイキストが最初に予想していたため、ナイキスト・シャノンの定理と言われたり、シャノンとほぼ同時期に、日本の染谷勲も発表していたため、染谷・シャノンの標本化定理とも言われます。

おまけ

駅馬車のところで、映画のコマ数が毎秒24コマと述べました。
現在のテレビは、毎秒30コマです。
テレビで映画は、このままではうまく再生できません。24コマから30コマへの変換が必要です。
この変換はどのように行われるのでしょう。
機会があれば、豆知識のコーナーに書いてみたいと思います。
筆者が少年の頃(中学だったか)に疑問に思って、NHKに問い合わせたら、この変換のしかたを、丁寧にレポート用紙に数枚の解説を書いてくれて送ってもらいました。