ラプラス変換とフーリエ変換については、以前、以下に述べました。

ラプラス変換とフーリエ変換

両者の長所と短所については、上のコラムに記載していますが、改めて再掲すると、

ラプラス変換の長所と短所
長所 : 変換の公式を用いれば、簡単に変換、逆変換ができる
短所 : 公式に当てはまらないと変換できない→公式に当てはめる工夫が必要

フーリエ変換の長所と短所
長所 : FFT を用いることにより簡単に数値計算ができる
短所 : 周期関数が必須→周期を設定すればよいので致命的ではない

のようになります。

フーリエ変換については、本コラムでも、2回に分けてFFTについて述べました。

エクセルによるFFT
エクセルによるFFT(その2)

分布定数線路の周波数特性については以下も参照ください。

分布定数線路の周波数特性
分布定数線路の周波数特性 続き

もう少し、ラプラス変換とフーリエ変換とを比較します。

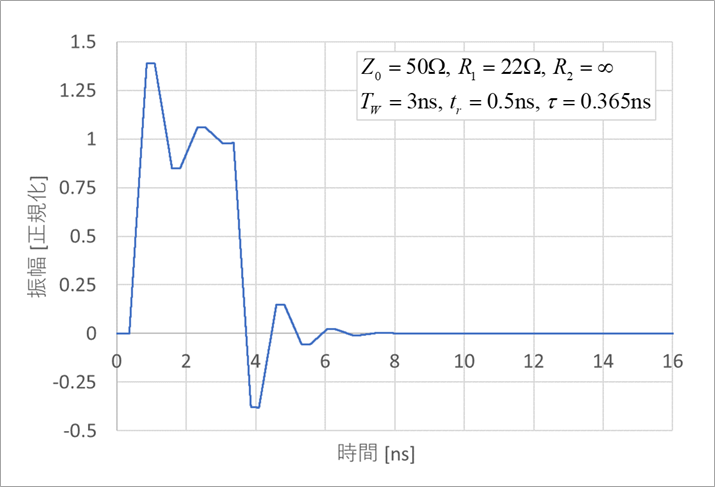
図1は、ある反射波形の例です。ドライバの出力抵抗 R1=22Ωで、12mAドライバに相当します。やや反射が大きい例です。パルス幅は3ns、ドライバの信号の立ち上がり時間は、0.5ns(0%-100%)、線路の遅延時間は0.365ns、およそ5cmを想定しています。

同じ回路をラプラスとフーリエで変換して、両者の波形の差を厳密に比較してみると、差が見られます。ただし、この差は、理論上の差で、実用上は問題になるようなものではありません。ただ、似たような比較をする場合に遭遇したときに応用できる手法と理解してください。

FFTのサンプル点Nは2の累乗、通常、256 または 1,024 程度に選びますが、ここでは、Nの影響を少なくするために、かなり大きな、16384(2の14乗)点に選びます。なお、時間から周波数への変換をフーリエ変換 FFT、その逆に、周波数から時間への変換を、逆フーリー変換 iFFT といいます。

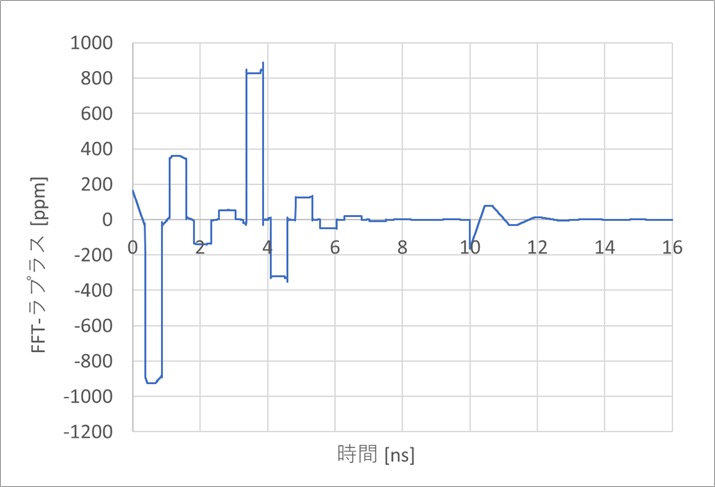
図2は、iFFTとラプラス変換の波形の差をプロットしたものです。差が小さいので，縦軸はppmで表しています。この差は、最大でも1,000ppm(0.1%)に達してないわずかなものです。

この差の理由は、ラプラスは、過渡現象で、フーリエは周期関数であるからです。すなわち、ラプラス変換は、時刻ゼロ(0)から現象がスタートします。一方、フーリエ変換は、過去からずっと同じ周期で現象が継続しています。反射波形は、反射が収まったように見えても、わずかながら反射が継続しています。

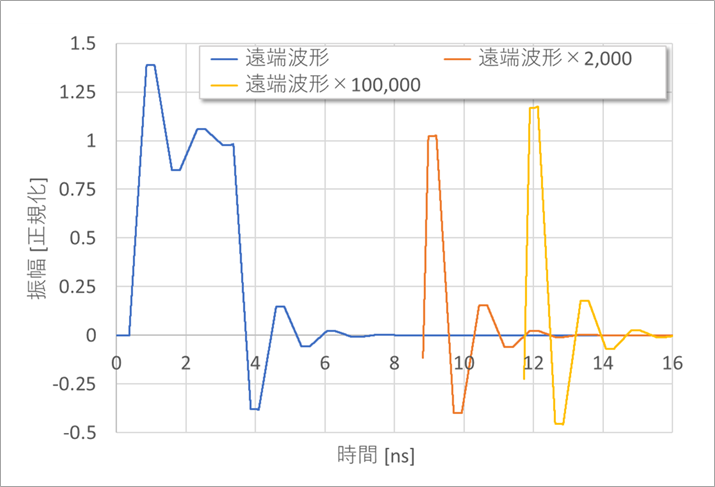
図3は、反射波形の、反射が収まったようにみえている部分を拡大して示したものです。9ns付近以降を2,000倍に拡大すると、まだ反射が継続しているし、さらに、12ns付近以降を100,000倍すると反射は継続していることが分かります。2,000倍や100,000倍して現れる反射の名残は、実際には何ら問題にはなりませんが、過渡現象と繰り返し波形とで、この程度の違いがあることを意識しておいてください。

ラプラスとフーリエを対等に比較するために、フーリエ変換の1周期 T を時刻 0 からスタートするラプラス変換に、時刻 T からスタートするラプラス変換を重畳させて、擬似的に周期化させます。

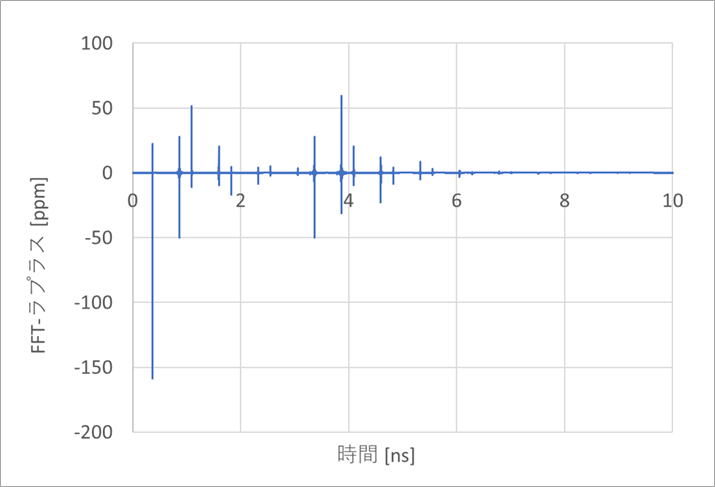
図4は、ラプラス変換の2周期目と16,384点iFFTとの差をプロットしたものです。同図は、図3の収まったかのような小さな反射を考慮したので、図2のような差はなくなりましたが、新たに、針状の誤差が現れました。

この針状の誤差の原因は何でしょう。

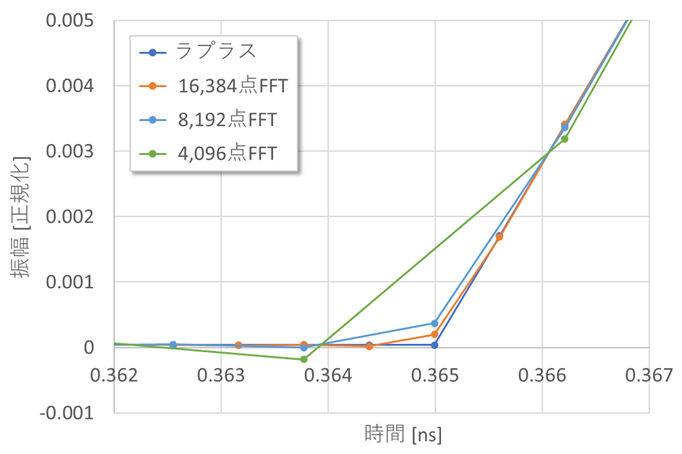
図4の最も差の大きいのは、最初の立ち上がり部です。図5は、この付近のフーリエとラプラスの解析結果を拡大して示したものです。図4は、iFFTは上述のようにN=16,384点ですが、図5では、N=16,384、N=8,192およびN=4,096について示しました。Nが小さいほど、ラプラスとの差が大きくなります。

ここでは、ラプラスは、折れ線で解析しました。折れ線の曲がり角は高い周波数成分を有しているので、iFFTでこれを忠実に解析するには、非常に大きなNを必要とします。折れ線は、原理の説明には有用ですが、実際の波形は、滑らかに変化します。滑らかな波形での比較については、また改めて述べることとします。