積分定数についての連立方程式

図1の式(1)に、積分定数A11～A22についての連立方程式を再掲します。
aijとbijの行列は、前回述べたとおりです。これも式(2)と式(3)に再掲します。
式(4)、式(5)のλ1、λ2などについては前回のコラムを参照ください。

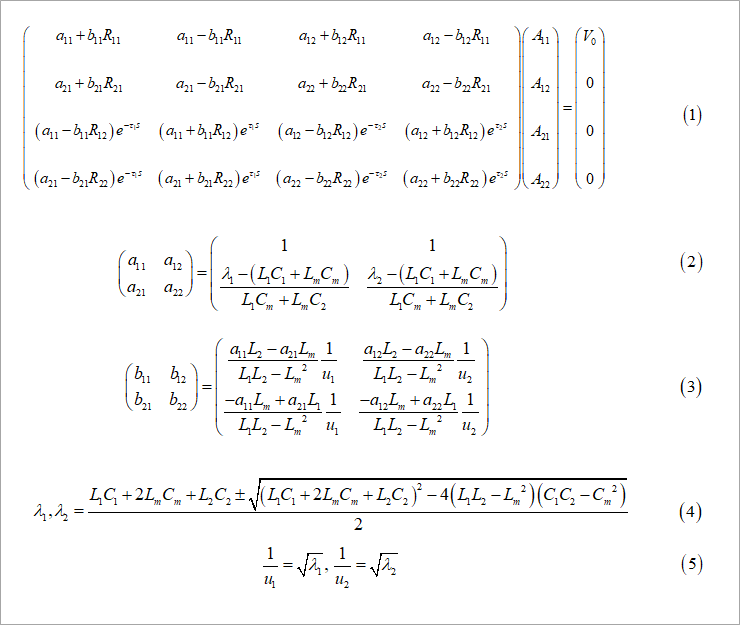
連立方程式の係数が煩雑なので、図2の式(6)に示すように、それぞれをPijと置いて表示します。左辺左の行列が係数で、次の列行列が未知数A11～A22、右辺が定数項です。連立方程式は、未知数が3つ(3元)までは、係数の行列式を、たすき掛け(Sarrus : サラスまたはサリュー)の方法で解きますが、4元以上になると、余因子を計算する必要があります。

この方程式は、右辺(定数項)が第1行だけで、他が0(ゼロ)なので少し簡単です。係数の行列の1行目に対する4つの余因子、すなわち、同図の式(7)に示すΔ11からΔ14だけですみます。Δ11は、係数の行列式の、1行1列から見た、すなわち、1行目と1列目を除いた小行列式です。行列式の性質から、Δijには、(-1)^(i+J)の符号が付きます。すなわち、Δ12とΔ14の符号はマイナスになります。未知数A11～A22は同図、式(8)のように求まります。

ここに、式(9)のΔは、上の方程式の係数の行列式で、時間τ1、τ2の組み合わせの指数で整理します。

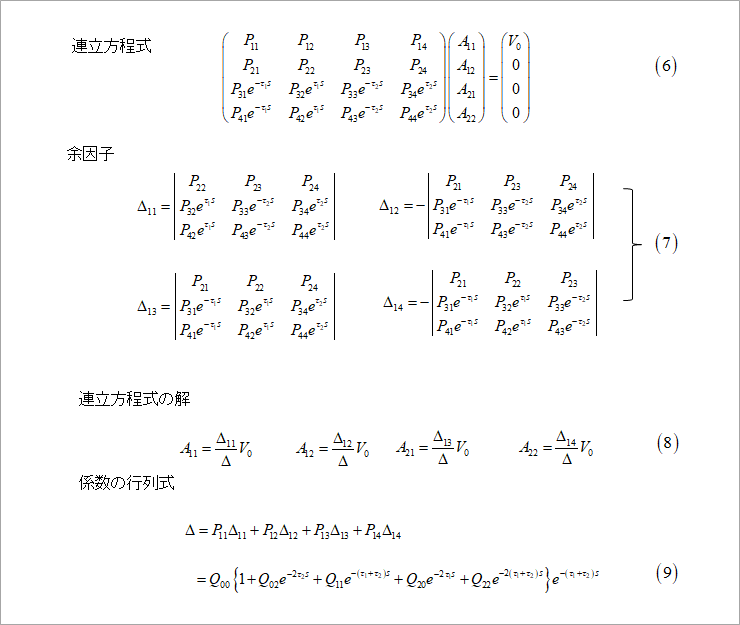
分数の級数展開

図2の式(9)のΔは、式(8)の分母で、図3の式(10)にしたがって級数展開します。また、exp(-τs)は、式(11)のように、ラプラス逆変換すると時間遅れになります。式(10)にしたがって、式(9)を式(12)のように級数展開します。

この分母の級数展開は、かなり煩雑で、解くには根気が必要です。式(10)の分母のxは、式(9)から分かるように、4つの項を含みます。これを2乗すると、4×4、すなわち16の項となります。信号の3往復まで考えると、3乗して4の3乗で64項、4往復だと、4乗で256項と莫大な計算量となります。

ただ、2乗の16項には、同じタイミングのデータが現れるので、実際には9項となります。この9項と、xの4項を掛けるので、36項となり、これも同じタイミングでまとめると、15項となります。さらに、式(12)を式(8)の各式に代入して、式(13)を得ます。通常は、クロストークの計算は、2往復で何とか実用になるでしょう。

式(13)で求めたA11～A22を用いて、近端と遠端の電圧を図4の式(14)のように求めます。同式のa11～a22は、図1の式(2)です。
式(14)を、式(15)のようにそれぞれの指数ごとにまとめます。
式(15)をラプラス逆変換すると、式(16)のように、信号源の時間遅れに係数をかけたものの和として表されます。
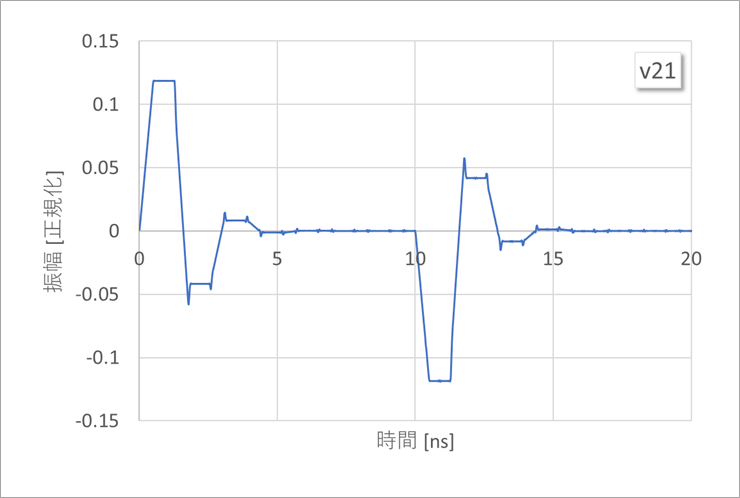
式(17)は、図5の回路のv21を計算した結果です。ここでは、2往復(4τ)まで記載しています。

以上の計算は、二つのモードの遅延時間が異なる表面層(マイクロストリップ線路)を前提にしています。二つのモードの遅延時間が等しい中間層(ストリップ線路)の場合、式(12)はかなり簡単になるので級数展開が楽になります。

解析例

図5は解析する際の回路です。線路#1および線路#2のパターン幅が、それぞれ、100umと200umの非対称線路です。
線路#1が加害者線路、線路#2が被害者線路で、両者の信号の向きが逆方向の近端クロストークv21を求めます。

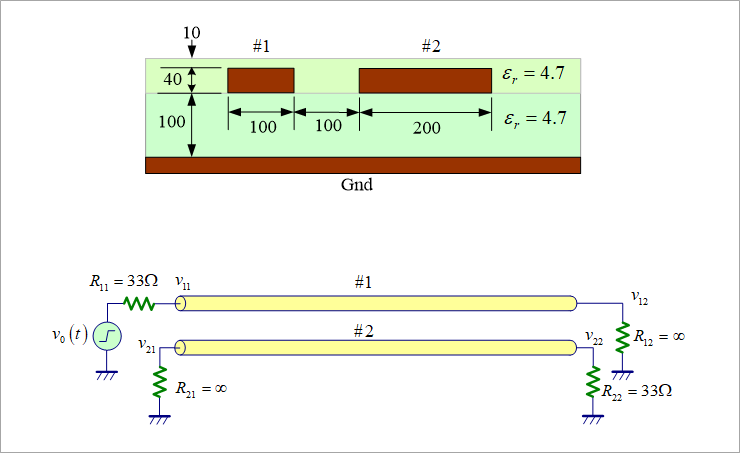
図4の式(17)の各項を図6(a)に図示します。ここに、信号源のv0(t)はステップ波形とします。
図6(b)は、その各項を加えたもので、これがv21すなわち近端クロストークです。
同図は、実際のクロストークとは異なるように見えます。これは、信号の立ち上がりが0(ゼロ)のステップ波形だからです。

なお、この例は、表面層(マイクロストリップ線路)なので、二つのモードの遅延時間の違いによって、ヒゲ状のノイズが生じますが、中間層(ストリップ線路)では、このヒゲは生じません。

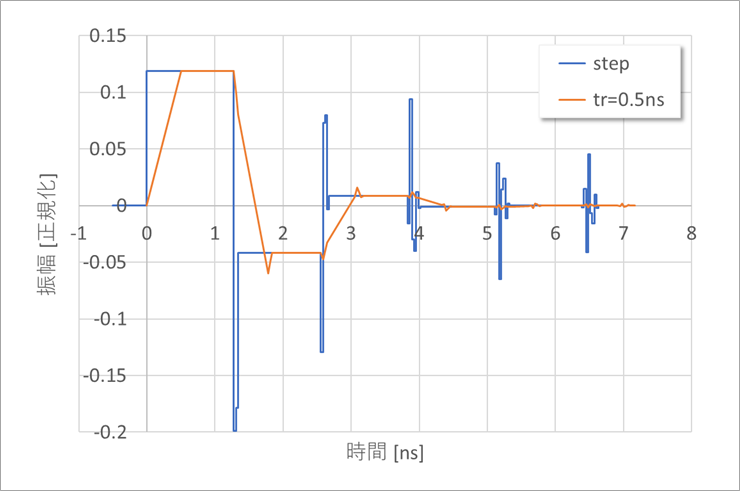
図7に、有限の立ち上がり、tr=0.5nsのときの(a)各項と、(b)各項の和を図6と同様に示します。
図6の急峻な狭いパルス幅が、立ち上がり時間に埋もれていることが分かります。
図6と図7とを比較して、ヒゲ状のパルスがどのように生じているか、実際には隠れているかを理解してください。

線路の一往復の、約1.3ns付近に、二つのモードの遅延時間の組み合わせ、すなわち、2τ1=1.339ns、τ1+τ2=1.308ns、2τ2=1.277のタイミングで振幅要素の加減算でヒゲ状のパルスとなっています。

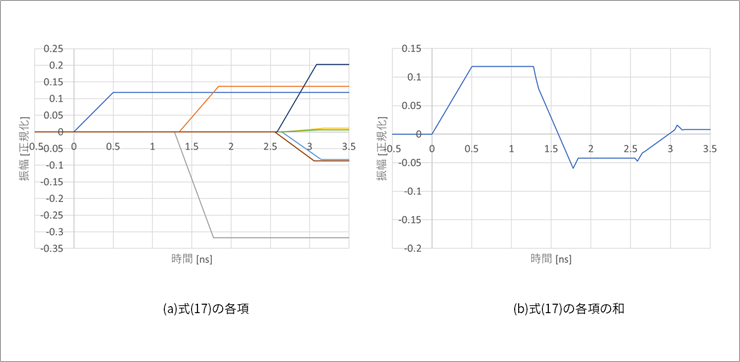
図8に、ステップ波形と、有限の立ち上がり、tr=0.5nsのときのv21を比較して示します。

近端、遠端の各部の波形

図9に、v21以外の近端と遠端の各部の波形を示します。

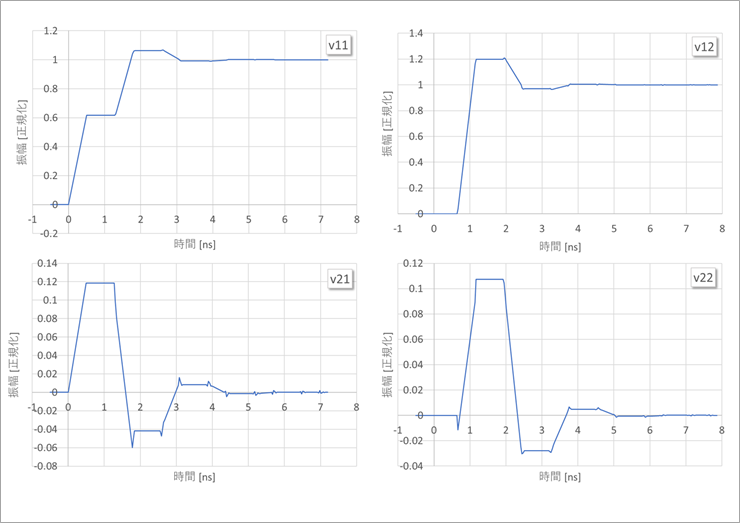
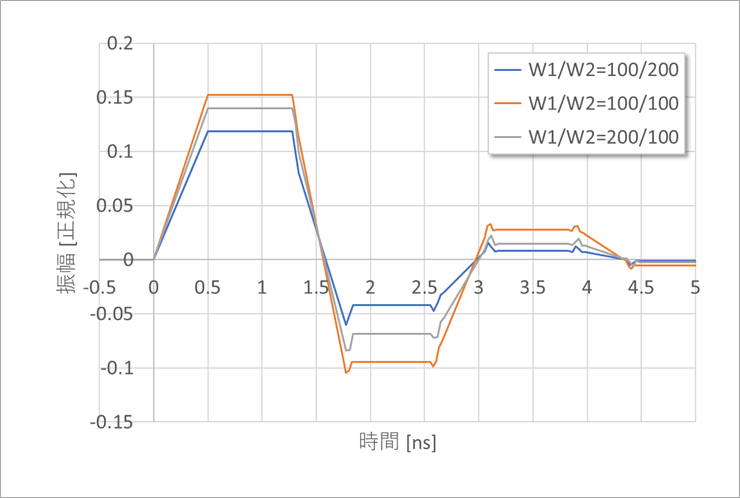
図10に、W1とW2とを変化させたときのV21を比較して示します。

フーリエ変換による方法

図1の式(1)のラプラス演算子のsをjωとおき、周期を設定するとフーリエ変換になります。
フーリエ変換については以下を参照ください。

ラプラス変換とフーリエ変換
https://www.macnica.co.jp/business/semiconductor/articles/basic/128001

エクセルによるFFT
https://www.macnica.co.jp/business/semiconductor/articles/basic/128345

エクセルによるFFT(その2)
https://www.macnica.co.jp/business/semiconductor/articles/basic/134557

図2の式(8)を求め、図3の式(12)のような級数展開をすることなく、式(13)を求めて信号源を与えてフーリエ逆変換すれば波形が求まります。

図11は、周期100ns、パルス幅10nsのときの、4096点FFTの解析結果です。

ラプラス変換による方法は、図3の式(12)の展開が最難関です。
ラプラス変換は、基本的に単発現象の解析で、フーリエ変換は、周期を想定します。

式ばかりだと実感が伴わないので、実際の解析例を図12、図13に示します。
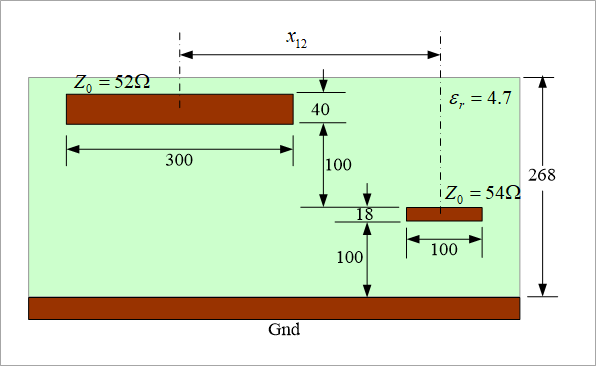
図12は、L3のグラウンド層の上に、L1とL2が存在する例です。
L1は、L3との距離が218umと大きいので、特性インピーダンスを、ほぼ50Ωにするために、パターン幅が300umとなります。その下のL2は、パターン幅100umで特性インピーダンスは、54Ωになります。

L1とL2との間は、層間のクロストークを考える必要があります。
層間のクロストークをCADで検証するのは、あまり簡単ではありません。(少なくとも過去は困難でした)

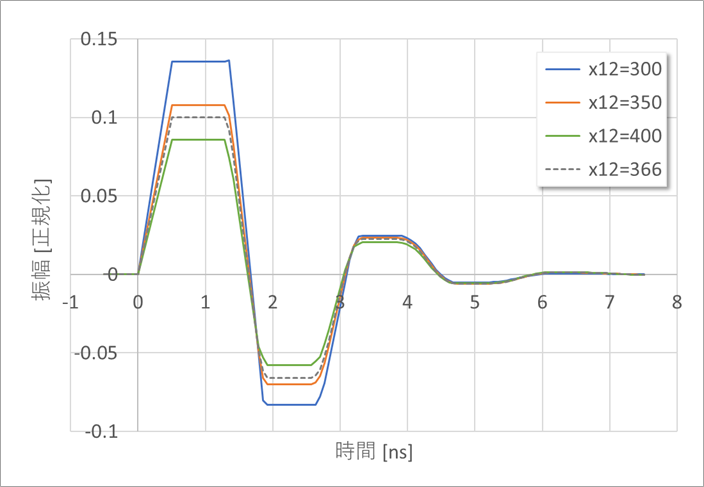
図13は、図12の断面図に対する、L1からL2への近端のクロストークを解析した例です。
図12のパターン間の中心距離を、300～400umと変化させて解析しました。
近端クロストークが、0.1になるときの中心距離は、366umとなりました。

このように、非対称線路の場合には、対称線路のときの、コモンとディファレンシャルの二つのモードに分解する方法がとれないため、計算がかなり煩雑になります。

次回は、固有ベクトルを用いた、少しスマートな解法について述べる予定です。