クロストークの数値解について、これまで以下のとおり2回に分けて述べました。
その1:
等価回路を元に、連立方程式を立てるところまで述べました。
かなり強引に、電圧と電流の関係を求めました。
その2:
この連立方程式を、ラプラス変換またはフーリエ変換で解く方法を述べました。
特にラプラス変換の級数展開は、相当の力業(ちからわざ)が必要でした。
今回(その3)はもう少しスマートに解く方法について述べます。
固有方程式と固有値
その1の図4の右上のラプラス変換した式からスタートします。
ここでは、図1の式(1)のように、ベクトル表記します。それぞれの変数や係数のベクトルを式(2)に示します。なお、ベクトルは、太字で示します。式(1)の電圧の式をxで微分して、電流の式を代入する、同様に、電流の式を微分して、電圧の式を代入すると、式(3)の2階の微分方程式を得ます。LCおよびCLを計算して、式(4)に示します。LCとCLは、互いに転置行列です。
転置行列とは、行と列とを入れ替えてできる行列です。ここでは、記号の前にtを上付けして表記します。二つの伝搬速度u1、u2は、その1の図5に示したように、4階の微分方程式を、記号Dを用いた記号解法により求めました。同図のλは、図1の式(5)のλに関する方程式(固有方程式)を解くことによって求まります。ここに、Eは単位行列です。
式(5)は、λに関する二次方程式なので、根の公式によりλを求めることができます。式(5)を展開して式(6)に示します。この式の根λ1およびλ2を固有値といいます。
式(5)から明らかなように、電圧と電流とは、同じ固有値を持ちます。
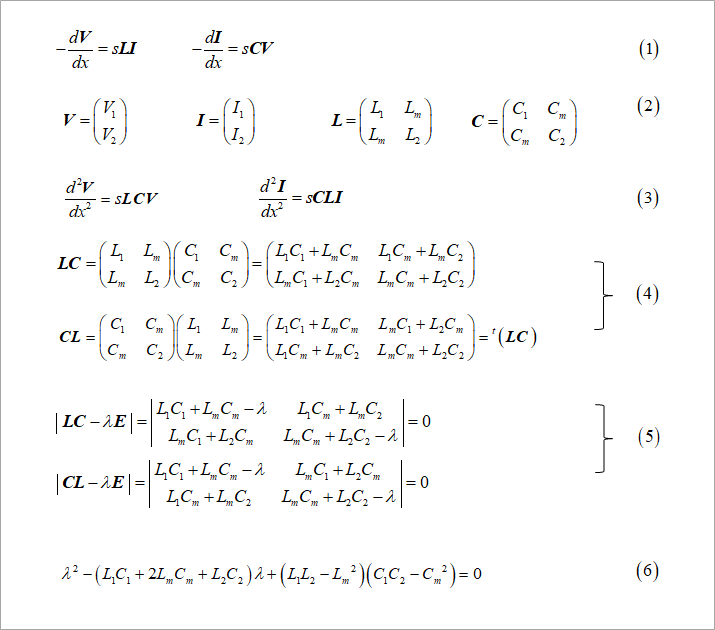
固有ベクトル
図2の式(7)は、この結合線路を伝搬する二つのモードの波を表します。これらを、ε1およびε2と名付けます。対称線路の場合、この二つのモードは、コモンとディファレンシャルの二つのモードに相当します。
ε1およびε2それぞれが、右行波と左向波の和(一次結合)で表されます。
A11~A22は、近端と遠端における境界条件から求まる微分方程式の積分定数です。式(8)は、二つの線路の電圧が、二つのモードの波の一次結合で表されることを意味します。式(9)は式(8)をベクトルで表したものです。ベクトル表記した、Aおよびεは、式(10)および式(11)です。式(8)の一次結合の係数、a11~a22は、その係数のサフィックスの最初の数字が線路で、2番目の数字がモードを表します。その1では、a11=a12=1としましたが、式(12)に示すように、それぞれのモードの、線路#1と線路#2の比で表されます。
この比を固有ベクトルといいます。
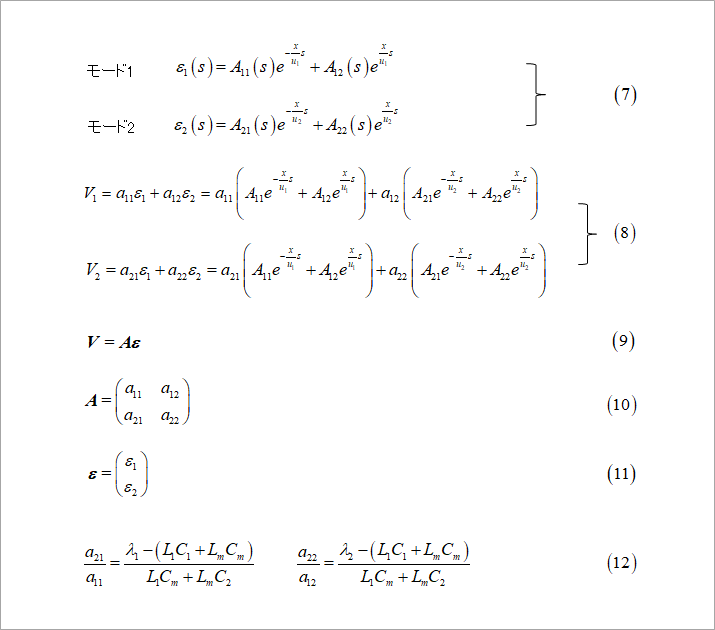
電圧の式と同様に、電流についても、図3にまとめます。式(7)に対応して、電流の二つのモードを式(13)に示します。電圧は、右行波と左行波の和ですが、電流は、向きがあるので、両者の差となります。中括弧内の差を、各モードの特性インピーダンスで除して、各モードの電流を求めます。式(8)に対応して、電流も、二つのモードの一次結合で表されます。
式(15)は、式(9)と同様に、式(14)をベクトル表記したものです。ベクトル表記した、Bおよびι(ギリシャ文字のイオタ)は、式(16)および式(17)です。電流についての方程式、図1、式(3)の、電流Iの係数CLは、電圧の式のLCの転置行列です。図1の式(4)をご覧ください。LCとCLの固有値が等しいことから、LCの2個の固有ベクトルよりなる行列Aと、CLの2個の固有ベクトルよりなる行列Bには、式(18)の関係があります。
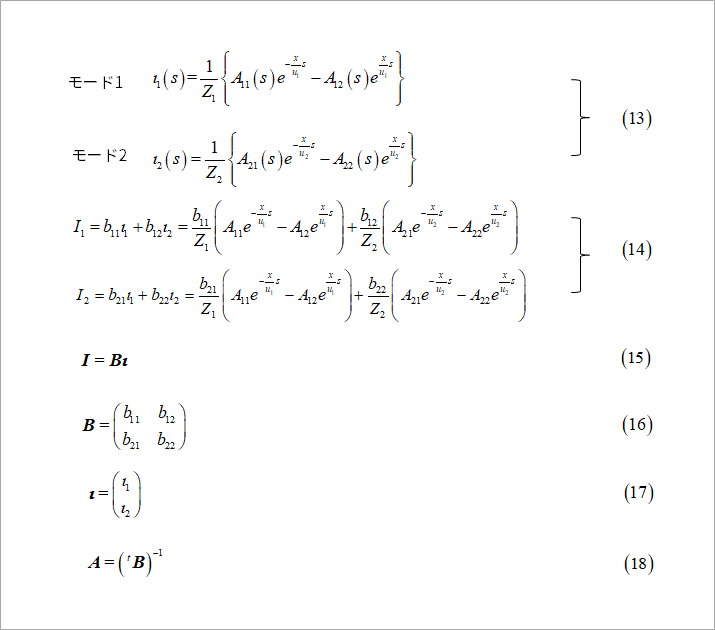
固有ベクトルは、その1の図6の計算により求めましたが、少しスマートには、図4の式(19)のx1、x2として、固有値、λ1、λ2について、それぞれ求めます。固有ベクトルは、式(20)のように、各モードごとに正規化しておきます。
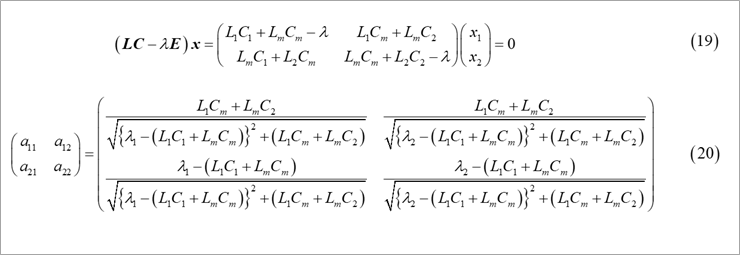
表1に、その2の図5の例で、実際に計算した例を示します。
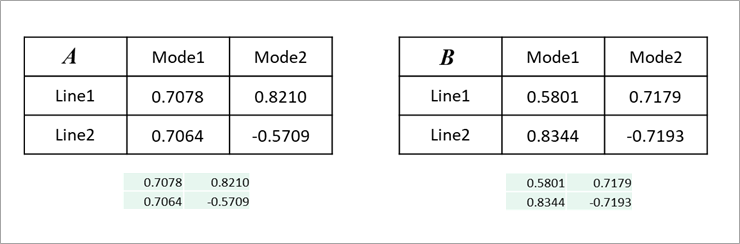
各モードの伝搬定数
各モードの伝搬定数を求めるのに必要な式を、図5にいくつか再掲します。
式(1)は、電圧と電流に関する基本式です。電圧と電流と、各モードの電圧と電流との関係は、式(9)と式(15)です。
式(1)と式(9)から、各モードの電圧と電流との関係は、式(21)のようになります。
式(1)の電圧の式と、式(21)とを比べてみると、ιの係数は、式(22)のように、各モードのインダクタンスl1(エル1)およびl2(エル2)となります。
同様に、式(1)と式(15)から、各モードの電流と電圧の関係は、式(23)のようになり、εの係数は、式(24)のように各モードのキャパシタンスc1およびc2となります。
式(22)および式(24)で求めた、インダクタンスとキャパシタンスから、式(25)のように、各モードの特性インピーダンスを求めます。
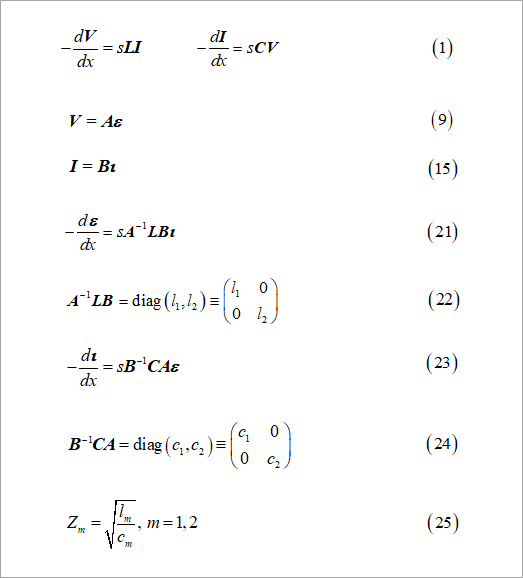
その1の図9と同様に、境界条件を与えて図6の方程式、式(26)を得ます。
各係数を、順に求めて、ラプラス変換かフーリエ変換で、近端と遠端の波形を計算します。
その1およびその2の係数と同じ記号(a11やb11)を用いていますが、当然値は異なるのでご注意ください。
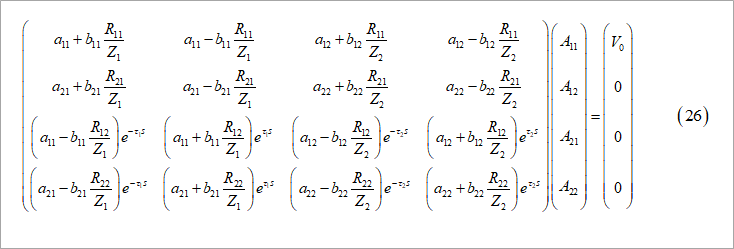
参考文献
碓井有三 :ボード設計者のための分布定数回路のすべて(第3版)自費出版, 2016
C.R.Paul : Analysis of Multiconductor Transmission Lines, 2E, Wiley-IEEE Press, 2007
碓井有三のスペシャリストコラムとは?
基礎の基礎といったレベルから入って、いまさら聞けないようなテーマや初心者向けのテーマ、さらには少し高級なレベルまでを含め、できる限り分かりやすく噛み砕いて述べている連載コラムです。
もしかしたら、他にも気になるテーマがあるかも知れませんよ!
