リアルタイム処理できるエクセルのFFT

エクセルに組み込まれている FFT については、以前紹介しました。
「エクセルによる FFT」を参照ください。

この組み込みの FFT は、バッチ処理の形をとり、使い勝手があまりよくありませんでした。
そこで、リアルタイムに処理できる FFT を作成したので紹介します。

FFTの簡単な応用

フーリエ変換や FFT というと少し難しい気がしますが、簡単な例でFFTを使ってみます。

図1は、ごく簡単な抵抗RとキャパシターC による積分回路です。
この回路にステップ波形を加えたときの応答を求めるには、オーソドックスには、ラプラス変換を用います。

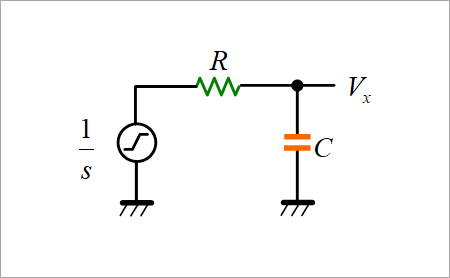
キャパシタのインピーダンス表示は、1/sCで、ステップ波形は1/sなので、図2に示す計算で比較的簡単に求めることができます。

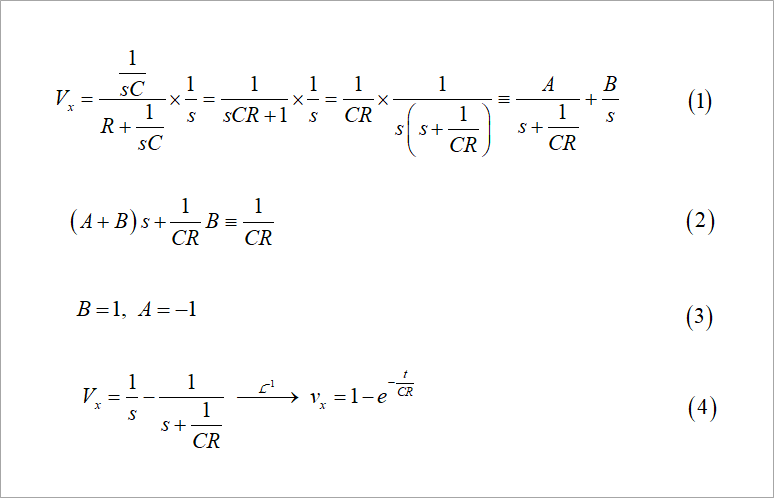
少し面倒なのが式(1)右辺の部分分数展開ですが、慣れるとそれほど難しくはありません。式(2)の恒等式により、sの次数ごとの係数を比較して式(3)のように A と B とを求めます。
求めた A と B とにより、式(4)が求まり、ラプラス逆変換して時間応答を求めることができます。
「ラプラス変換とフーリエ変換」の図3を参照ください。

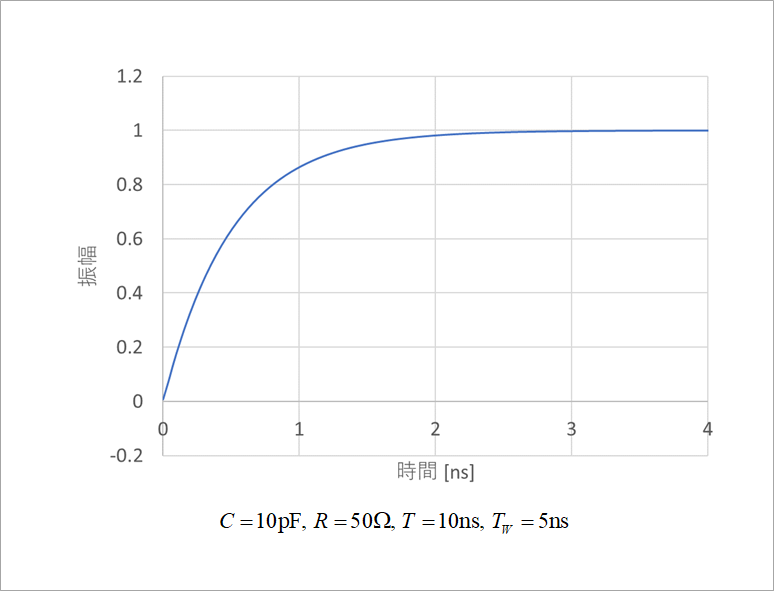
図3は、その計算結果です。

ラプラス変換でも簡単に解けますが、例えば、LCR 回路のように少し複雑になると、部分分数展開が複雑になって、さらに振動モードや減衰モードに場合を分けるなどの操作か入るので、面倒になってきます。

ここで、ラプラス変換とフーリエ変換とは、積分の形が非常に似ているので、ラプラス変換の演算子のsをjωと置き換えるて周期で割るとフーリエ変換になります。
数学的には両者は別物ですが、回路を解く上では両者は親戚のようなものと考えればよいでしょう。(数学の専門家には叱られそうですが)

「ラプラス変換とフーリエ変換」を参照ください。

図4の式(5)に示すように、Vx を伝達関数 F(s)と信号源 V0(s)との積と考えます。
F(s) のsをjωとおくと、F(ω) は式(7)となります。
信号源は、フーリエ変換では周期を考えるので、図4の式(8)のように表されます。

この周波数関数を FFT により時間関数に変換します。

リアルタイム処理の FFT は以下にアップロードしています。
http://radioy.a.la9.jp/tool/tool.htm

または直接
http://radioy.a.la9.jp/tool/FFT256.xlsx

信号源は、矩形波と台形波の二つをあらかじめ用意しています。

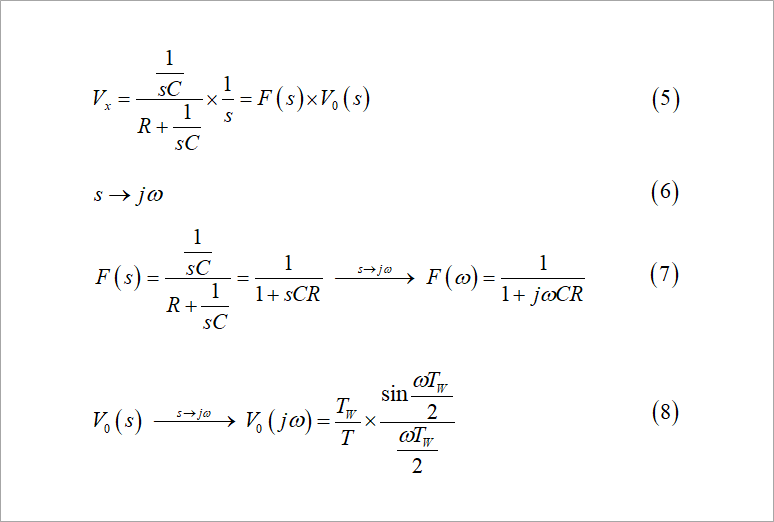
ステップ応答を求めるには矩形波を使います。
「sample」のシートのCR 積分回路の「C」と「R」に値を入力します。
E列は、伝達関数F(jω)と信号源のV0(jω)の積を計算しています。
このωの関数の先頭のセルを「波形」シートの「A2」に絶対参照の形で引用してください。この例だと「=sample!$E$4」です。
この時間波形が図5です
CR の値と信号源の T や TW を適当に選択してください。

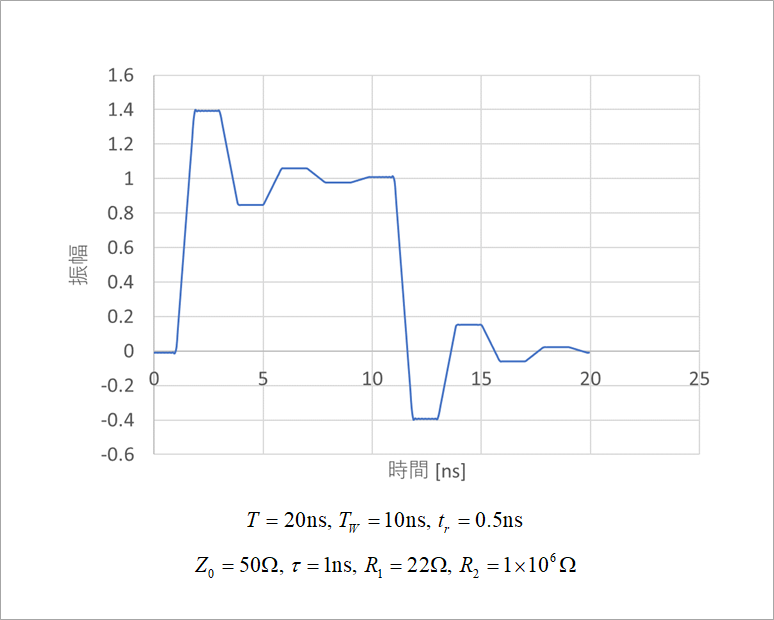
次に、分布定数回路の反射波形を求めます。
「縦続行列」の図3に分布定数回路の伝達関数Fを記載しています。
この式をエクセルシートのsampleで計算しています。
特性インピーダンス Z0、線路長(遅延時間)τ、ドライバの出力抵抗R1、レシーバの終端抵抗R2を与えて、J列に伝達関数と信号源の積を計算しています。
信号源は、「信号源」シートの台形波を用いています。

このωの関数をフーリエ逆変換します。
「波形」シートの「A2」に絶対参照の形で引用します。すなわち、「=sample!$J$4」です。

FFT を用いれば、回路の応答を周波数関数で表現できればFFTを用いたフーリエ逆変換で時間関数に変換することができます。

複雑な LCR の共振を含むような回路もラプラス変換で得場合には、減衰モードと振動モードの場合分けが必要でしたが、簡単に変換してくれます。
この FFT の応用については、何回かに分けて続編の掲載を予定しています。

こんな回路でも解けるのかなどのご意見をいただけると幸いです。