リップル・フィルタとは?
AC 電源を整流すると、「脈流になること」と「この脈流を直流にするために平滑回路を用いること」は
『交流(AC)電源と直流(DC)電源』で述べました。この平滑回路は、一種のローパス・フィルタです。このフィルタは、直流電圧に重畳したさざ波(Ripple:リップル)のような成分を抑制するという意味でリップル・フィルタと呼ばれます。
ローパス・フィルタは LC または RC で構成しますが、電流の経路に R が入ると電圧ドロップが生じるので、特に小電力の場合以外には LC を用います。
なお、以下はリップル・フィルタの原理について述べています。実際の回路では後段にレギュレータを用いるために、もっと簡単なリップル・フィルタで済ませたり、高い周波数ではレギュレータでは除去できない高周波成分を除去するために、レギュレータの後段に用いることもあります。
LC によるローパス・フィルタ
L と C とを縦続に接続することによって、ローパス・フィルタを形成します。図1 は、その基本の 2次ローパス・フィルタです。
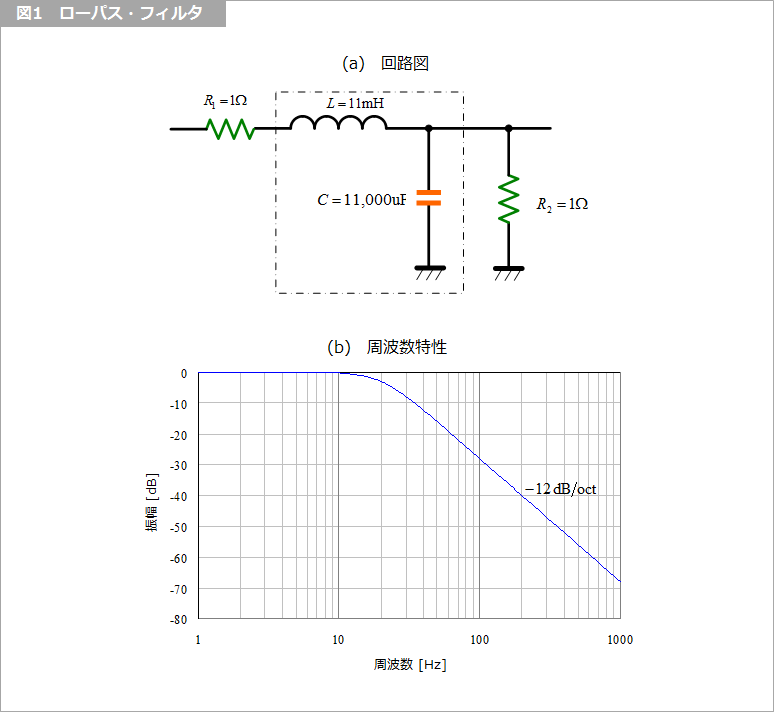
フィルタは、基本的にインピーダンスとカットオフ周波数とで特性を決定します。アナログ信号に用いるフィルタの場合にはインピーダンス整合を重要視しますが、リップル・フィルタの場合にはそれほど考慮しません。
図1 の回路の場合、インピーダンスは Z = √(L/C) で、カットオフ周波数は ωC = √(2/LC) で表されます。
例えば、インピーダンスが 1 Ω でカットオフ周波数が 20 Hz の場合には、L = 11 mH、C = 11,000 uFとなります。
2次フィルタなので、ロールオフ特性は -12 dB/oct(脚注1)となります。L-C-L または C-L-C と縦続接続すると 3次フィルタとなり、さらに段数を増やすと高次のフィルタが実現できます。
小電力の場合には R と C とでフィルタを構成することもありますが、多段に接続しても通常の意味での次数が増えるわけではありません。
脈流とローパス・フィルタ
図2 に脈流の周波数スペクトルと 2次ローパス・フィルタを通したときのスペクトルの変化を示します。実際の整流回路と平滑回路との組み合わせではダイオードを介しているため、図2 のような単純なスペクトルにはなりませんが、およその傾向を示しているとしてご覧ください。
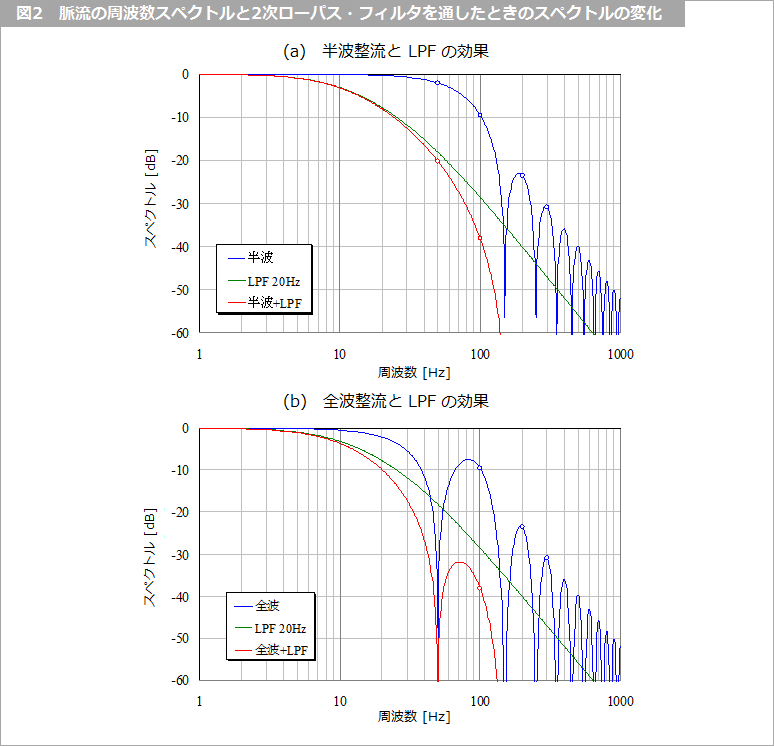
図2(a) は半波整流波形の場合で、基本波の 50 Hz の成分が、-2 ~-18 dB に 16 dB 減衰しています。
図2(b) は全波整流波形の場合で、最も低い周波数成分は 100 Hz ですが、28 dB 程度減衰しています。
フィルタのカットオフ周波数を 50 Hz に選ぶと、特に半波整流の場合には基本波の 50 Hz はほとんど減衰できていません。
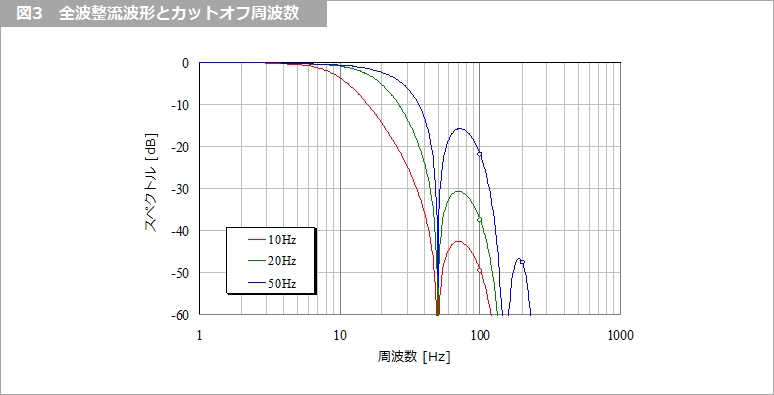
図3 にカットオフ周波数を、10 Hz、20 Hz、50 Hz と変えた場合の全波整流の場合のスペクトルの変化を示します。十分に低いカットオフ周波数が必要なことがわかります。
キャパシタとインダクタを小さくするには
上述したのは、商用周波数の場合です。周波数は 50 Hz または 60 Hz なので、この周波数の脈流の成分をカットするのに十分なフィルタのカットオフ周波数を得るには、キャパシタとインダクタの両方の値を大きくする必要があります。例としてあげた 11 mH のインダクタや 11,000 uF のキャパシタは実現が難しかったり、極端に大きくなったりします。
これらの値は、周波数にそれぞれ反比例(脚注2)するので、500 kHz なら 50 Hz の 10,000分の1 となって、1.1 uH と 1.1 uF と実用的にも問題のない領域に入ってきます。
前回、スイッチング方式の周波数を数 100 kHz ~ 数 MHz に選ぶと述べましたが、リップル・フィルタの面からみても有利となることがわかります。
脚注1
「oct」は、音楽のオクターブの意味で、2倍の周波数を意味します。すなわち、周波数が 2倍になると、振幅は -12 dB(4分の1)になります。同じ特性を、-40 dB/dec とも表現できます。「dec」は 10倍を意味し、周波数が 1桁高くなると、振幅は -40 dB(100分の1)になります。
脚注2
L と C の値の積の平方根が周波数に反比例します。
碓井有三のスペシャリストコラムとは?
基礎の基礎といったレベルから入って、いまさら聞けないようなテーマや初心者向けのテーマ、さらには少し高級なレベルまでを含め、できる限り分かりやすく噛み砕いて述べている連載コラムです。
もしかしたら、他にも気になるテーマがあるかも知れませんよ!

