ステップ応答

その1で述べた、フィルターを通したときの信号波形について述べます。
時間応答を求めるために、ここでは、フーリエ逆変換を用います。
図の番号は、その1、その2で通しでつけています。

その1は以下です。

ベッセルフィルターと他のフィルターの違い その1

図10に、図4の各フィルターにステップ波形(立ち上がり時間 tr=0)を加えたときの時間応答を示します。(フィルターの次数は7)

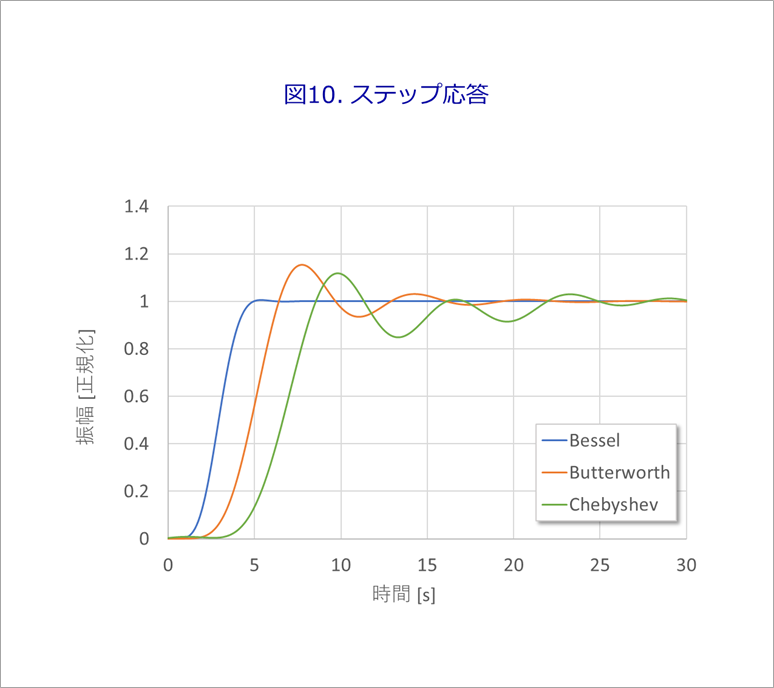
それぞれのフィルターは、図9の群遅延の暴れに対応して、波形が乱れていることが分かります。

反射やクロストークの波形解析の際に、折れ線(ランプ)の波形をよく用います。

実際の波形は、折れ線ではなく、角(かど)が滑らかに変化します。

図10に示すように、ステップ波形をベッセルのLPFを通すことにより、滑らかな、きれいな波形を得ることができます。
ベッセル以外のフィルターでは、オーバシュートやリンギングが生じるのでこの用途には適していません。
それぞれの波形の遅延時間は、ほぼ図9の群遅延の時間に相当します。

パルス波形の立ち上がり時間

パルス波形の立ち上がり時間は、フル振幅の10%-90%、または、20%-80%で定義されることが多いですが、折れ線のランプ波形では、0%-100%で定義します。
ここでは、フィルターを通した波形の、20%と80%の2点を通るランプ波形を推測して、そのランプ波形の0%-100%で定義します。

図11は、図10のベッセルの波形の立ち上がり部を拡大して、20%と80%の点を通るランプ波形を推測したものです。
なお、群遅延分を考慮して、ランプ波形が、0(ゼロ)から立ち上がるように補正しています。

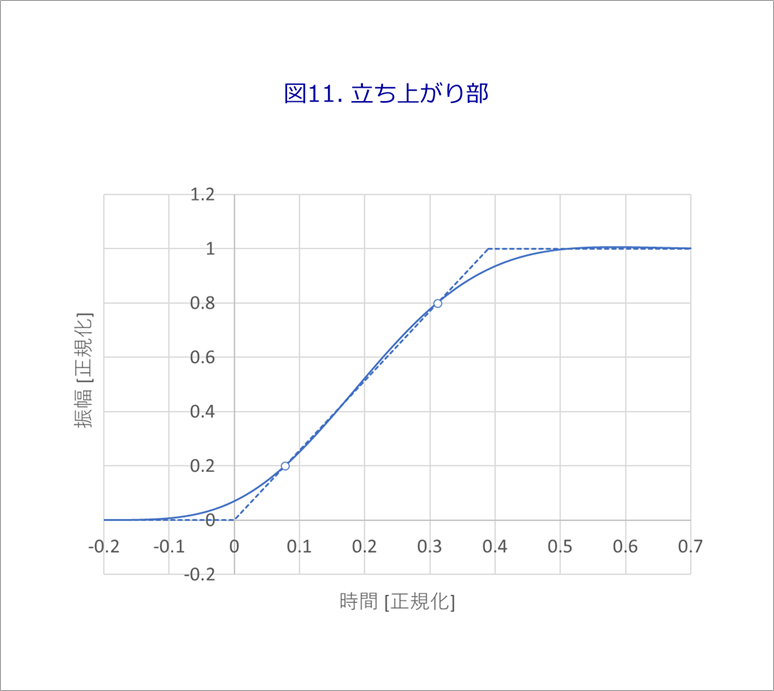
図は、遮断周波数fcを1に正規化しています。このときの0%-100%の立ち上がり時間trは、0.3894です。fcとtrとは互いに反比例します。すなわち、fc×tr=0.3894です。
例えば、立ち上がり時間を0.5にするには、fc=0.3894/0.5=0.779です。
このfc×trの積は、ベッセルの2次から8次に対して、0.38から0.39の間の値をとります。[脚注5]

図12(a)に、図10の次数nを2から8まで変化させたたときの立ち上がり波形を重ねて示します。

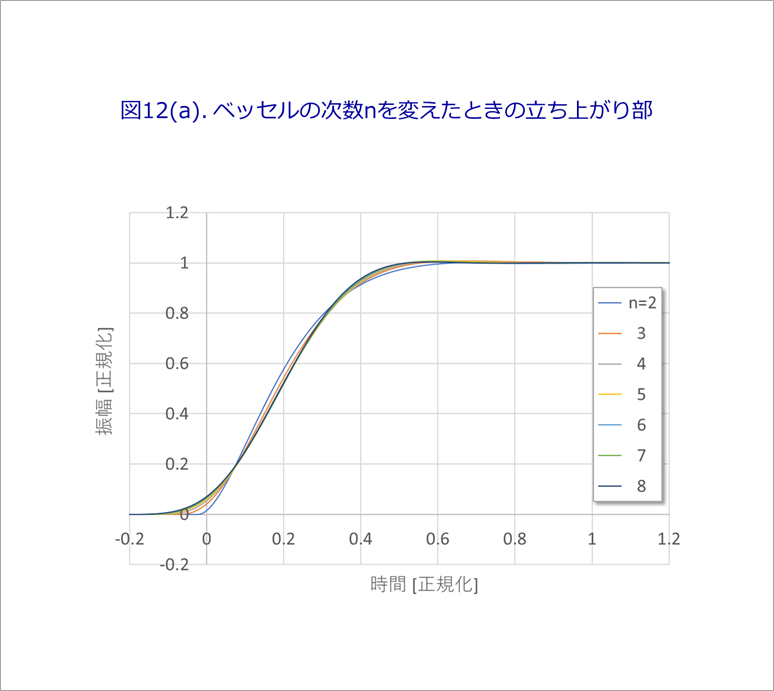
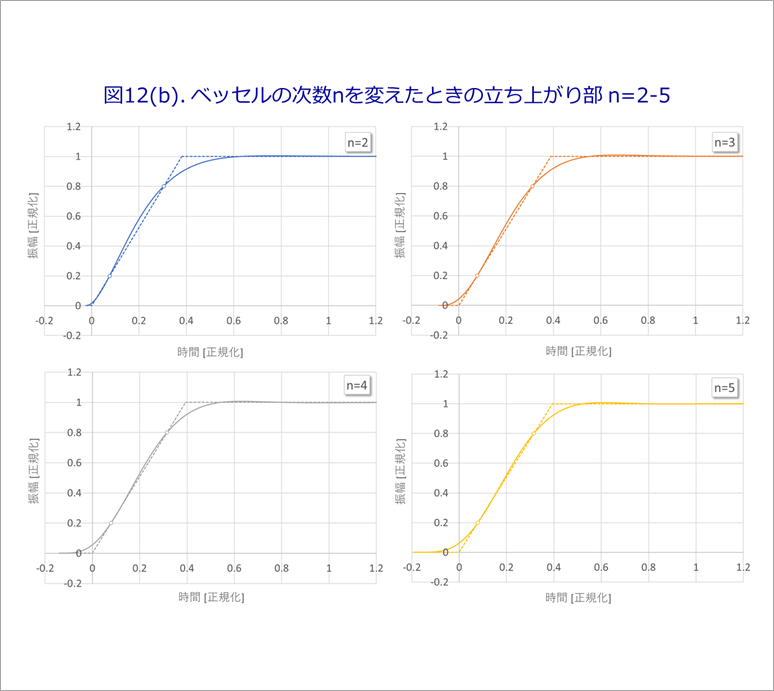
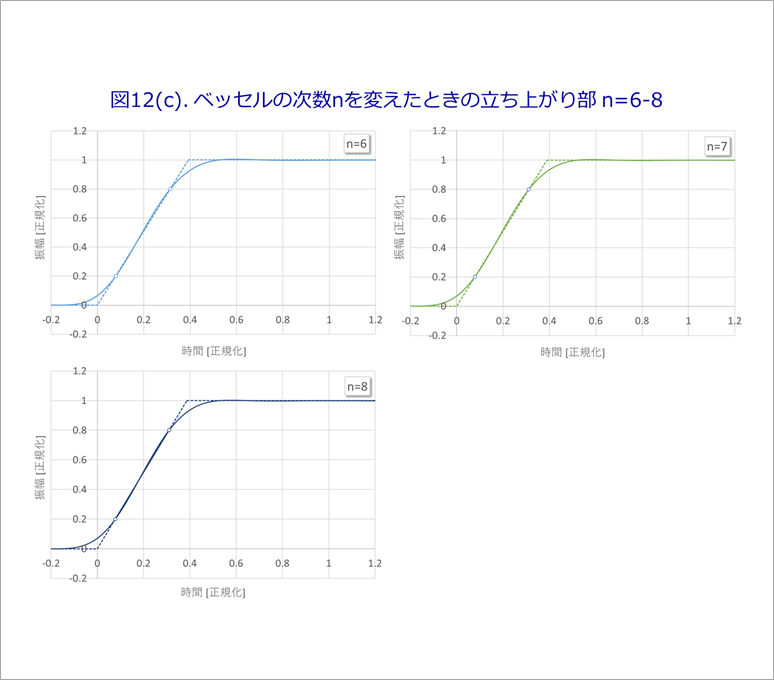
n=2では、立ち上がりの直線部がややふくらんでいますが、n≧3では、20%-80%の部分はほぼ直線とみなすことができます。
図12(b)は、n=2-5の場合を、図12(c)は、n=6-8の場合をプロットを分けて示します。

以上は、周波数を1に正規化しています。以下、実際の時間と周波数の例を示します。

立ち上がり時間を0.5nsにするにはfc=0.3894/0.5ns=779MHzです。
このときの周波数特性を図13に示します。

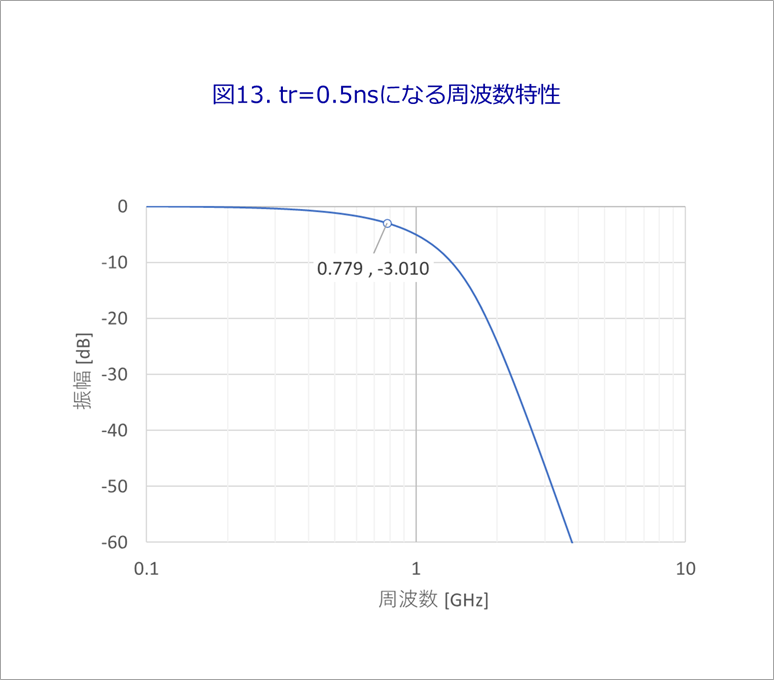
図14は、図13の特性に立ち上がり時間ゼロの矩形波を通したときの応答で、図15は、その立ち上がり部の拡大です。

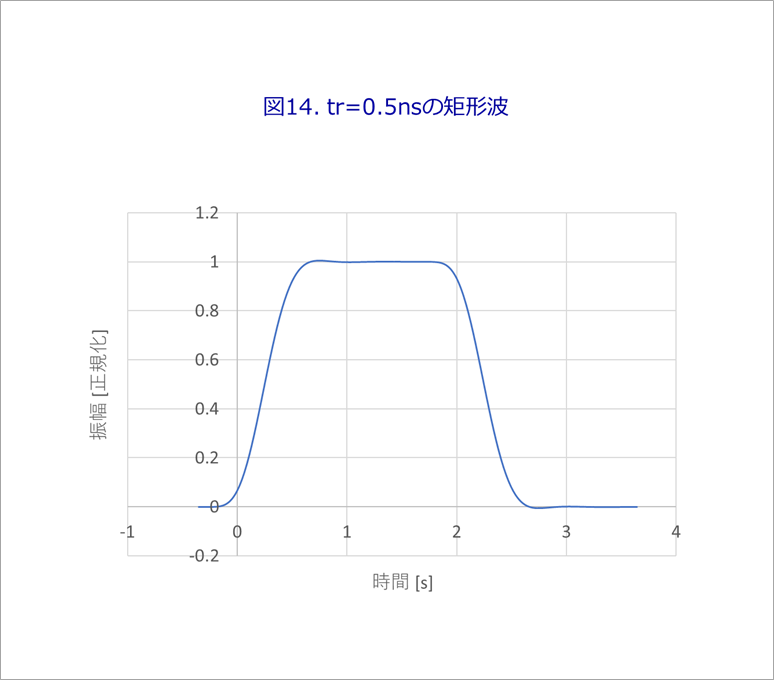
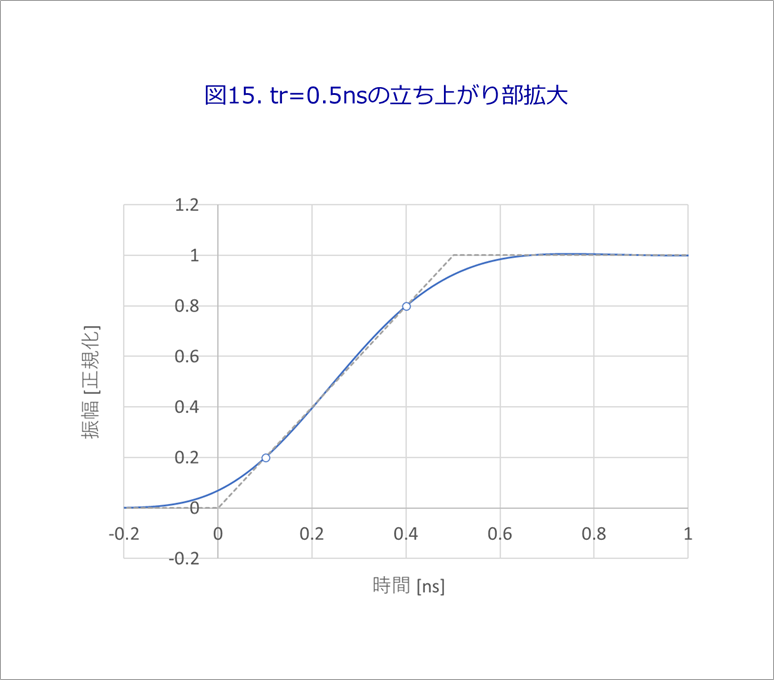
以上のように、折れ線の波形の時間応答に対して、ベッセルフィルターを通した、立ち上がりゼロのステップ波形や矩形波を通したものを信号源とすると、より実際に近い時間応答を得ることができます。

また、例えば、周波数帯域が7GHzのオシロスコープの観測波形は、アンチ・エイリアス・フィルターとして7次のベッセルフィルターを用いているとすると、立ち上がり時間がゼロの波形でも、tr=0.3894/7GHz=56psの立ち上がり時間となります。

立ち上がりが有限なパルス波形を、ある帯域のオシロスコープで観測すると、元の波形の立ち上がり時間より大きくなります。
この観測したときの立ち上がり時間は、経験的に、帯域が持つ立ち上がり時間と元の立ち上がり時間との自乗和であると言われています。

図16はこれを検証した結果です。

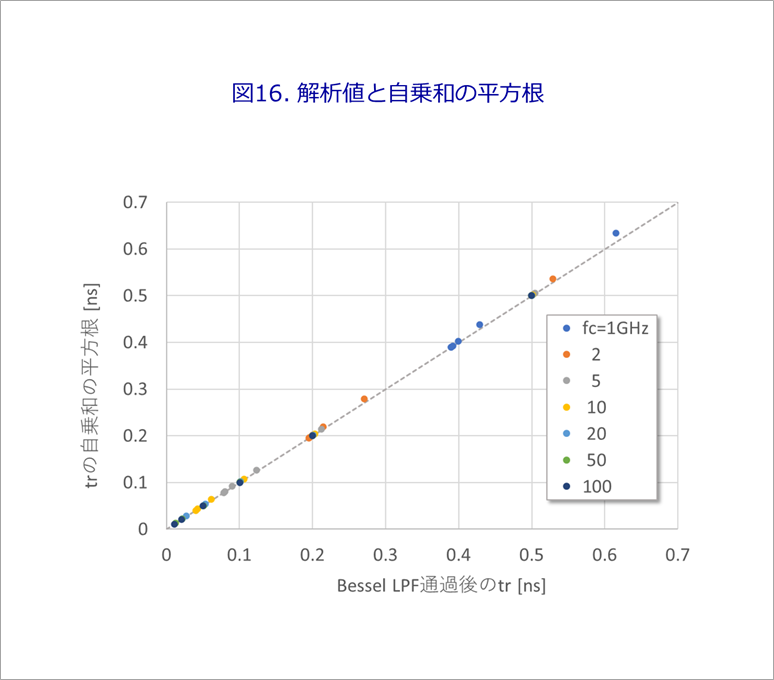
パルス波形の立ち上がり時間をtr0、この波形をベッセルフィルターに通したときの立ち上がり時間をtr、オシロスコープの帯域から決まる立ち上がり時間を、tr1(=0.3894/帯域)としたとき、横軸はtr、縦軸は、自乗和の平方根、すなわち√(tr0^2+tr1^2)です。
経験的な自乗和にほぼ一致していることが分かりました。
ここに、tr0=10ps～500ps、オシロスコープの帯域(ベッセルフィルターのfc)は、1GHz～100GHzで計算しました。

脚注5
fc×trは、0.35と言われていることが多いですが、これは、ステップ波形をCRの1次遅れ回路に通したときの、10%-90%の場合を表しています。
簡単に求めることができるので、計算してみてください。

この計算は、「豆知識」の、
オシロスコープの周波数帯域と信号の立ち上がり時間
に述べています。

なお、本稿では、trを0%-100%で定義しているので、0.38から0.39は、0.8を掛けて、ほぼ0.3程度になります。