降圧（ステップダウン）型

例えば、8 V の電源から 5 V を得るには、リニア方式でも実現できます。ただ、『リニア方式レギュレータ』で述べたように、リニア方式は損失が多く、出力電圧が低くなると効率の低下が顕著になってきます。近年の電源電圧の低電圧化に伴って、リニア方式は主電源用にはあまり用いられなくなってきました。

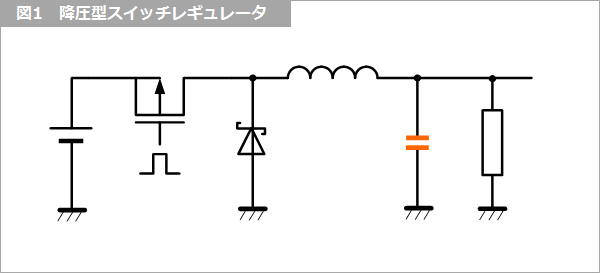
降圧型の基本回路は、『電圧レギュレータ』の 図3 に示すとおりです。実際の回路は、以下の 図1 に示すように、S1 は MOS トランジスタ、S2 はダイオードを用います。

この回路の解析は、

1. 『電圧レギュレータ』の 図3 の基本回路を SPICE で解析
2. ラプラス変換による過渡現象の解析
3. または、S1、S2 のスイッチの組み合わせをパルス列にして高速フーリエ変換（FFT）解析

などが考えられます。1 は SPICE が使える人なら比較的簡単に解析できるでしょうから、2 と 3 について解説します。当然ながら、いずれの解析方法も同じ結果を得ます。

ラプラス変換による過渡現象の解析

図2 のように i1 と i2 の 2つの網電流に対して、方程式を立てます。

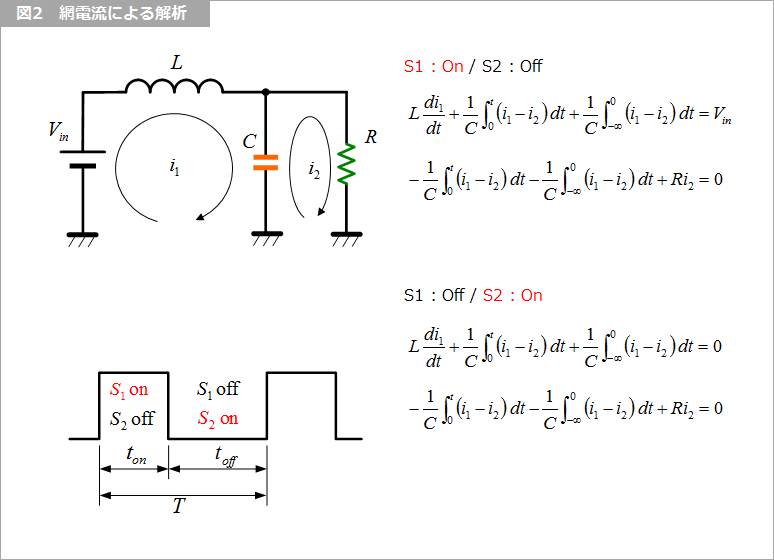
この微分方程式をラプラス変換して、連立方程式を解いて 2つの電流を求め、ラプラス逆変換します。RLC の過渡現象は回路定数により、サイン、コサインの組み合わせの振動型と、指数関数で表される減衰型とにわかれます。

解は少し煩雑なので、別に示します。
特別号：ステップダウン型の過渡現象の解

S1 がオン（S2 がオフ）のときの電流を求め、これらの電流を初期値として S2 がオフのときの電流を求める、その繰り返しにより、電源投入時の出力電圧の変化を求めることができます。図3 はその解析結果の例と、i1、i2の近似解です。i1 は、S1 がオンのときに増加し、オフになると減少しながら、全体的に増加を続けます。i2 は i1 のように凸凹ではなく、単調に増加を続けます。

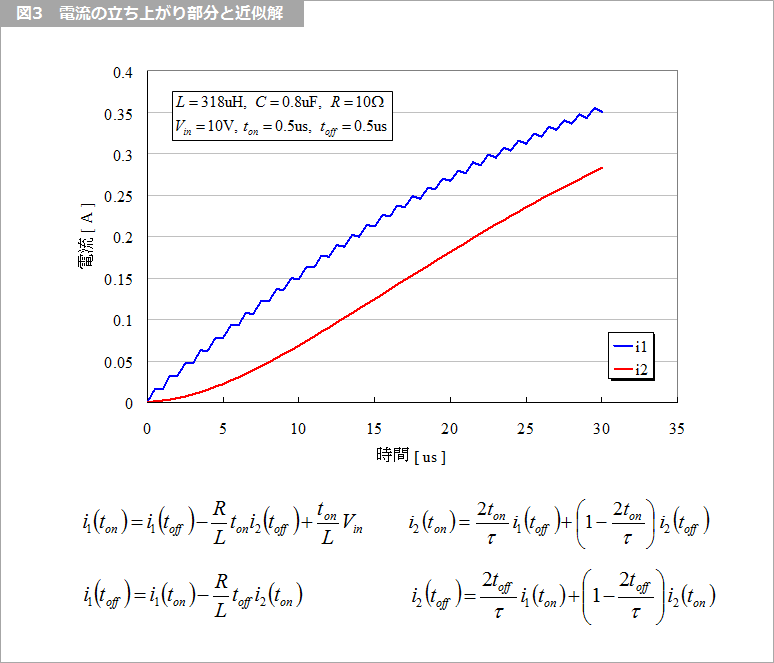
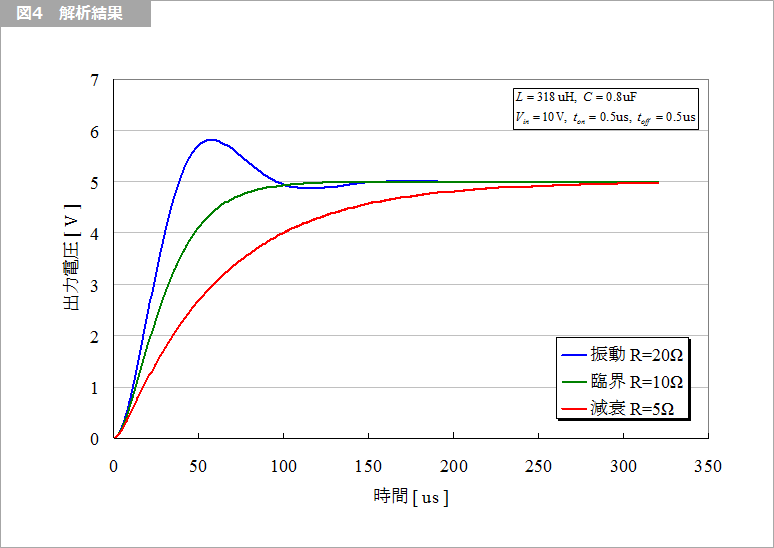
図4 は、異なる負荷抵抗による出力電圧の立ち上がりの様子を示します。負荷が軽い（抵抗が大きい）と立ち上がり時にオーバシュートが生じることがあるので、要注意です。

FFT 解析

図5 に、図2 の回路の伝達関数を求めて示します。

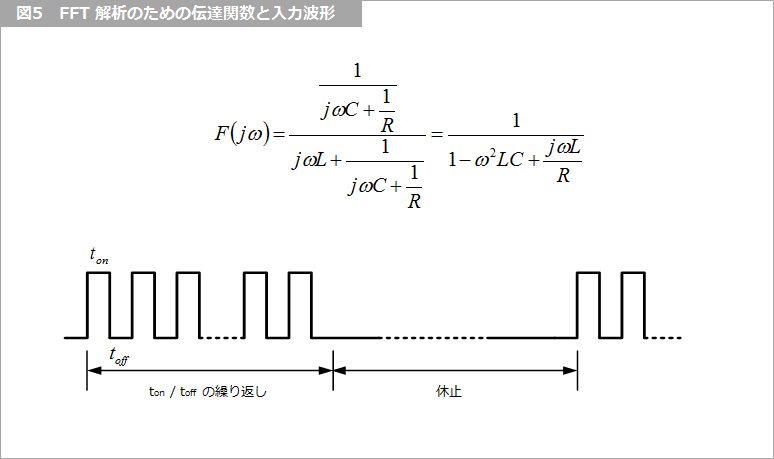
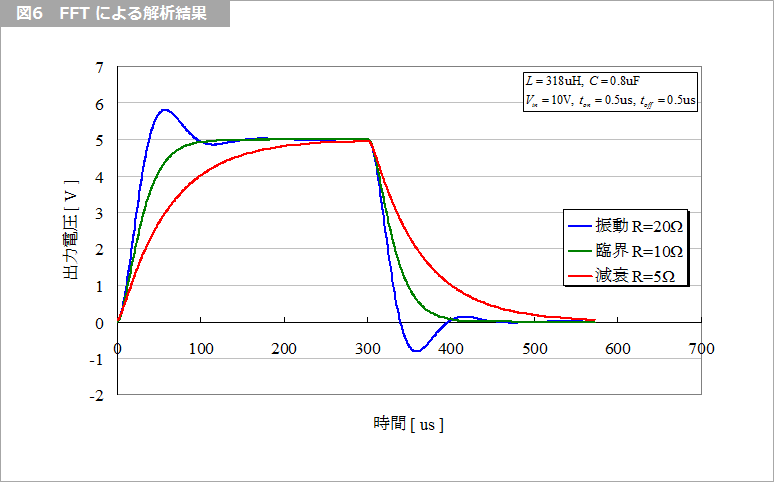
FFT で過渡解析を行うために、図5 に示す入力を与えます。ton と toff による繰り返し波形を出力波形が安定する回数繰り返して、同じ時間だけ休止する時間を設定します。図6 に FFT による解析結果を示します。この解析には 4,096 点の FFT を用いました。

上記いずれの解析の場合でも、出力電圧を求めることができますが、いずれも「数値解」です。それでは、「解析的に」あるいは「代数的」に解くにはどのようにすればよいでしょうか。『スイッチング方式レギュレータ～その2』でに詳しく述べることにします。