NVIDIA DGX™ B200で始めるNVFP4推論　～第1話:NVFP4とは～ - 半導体事業

条件を指定して絞り込む

現在2032件がヒットしています。check

基礎 NVIDIA

はじめに

大規模言語モデル(LLM)が大型化し、それらを活用したアプリケーションが複雑化する中で、計算量の削減や推論時間の短縮は重要な課題です。　　

NVIDIA® DGX™ B200をはじめとする最新のNVIDIA Blackwell世代GPUでは新たに4ビット浮動小数点(FP4)型が新たにサポートされ、計算量の削減や推論時間の短縮が期待できます。　　

本連載では全5話に渡ってBlackwell世代のGPUから新たに対応したNVFP4と呼ばれる形式にLLMを量子化し、NVIDIA社の推論用マイクロサービスであるNVIDIA® NIM™へデプロイし推論する方法やNVIDIA TensorRT™-LLM Python APIを用いて推論する方法に関して解説します。　　

第1話である本記事ではBlackwell世代のGPUから対応したNVFP4について説明します。

[NVIDIA DGX B200で始めるNVFP4推論]

第1話　NVFP4とは

第2話　NVIDIA® TensorRT™ Model Optimizerを使用した量子化

第3話　Multi-LLM NIMでの推論

第4話　NVFP4とFP8のベンチマーク測定

第5話　Llama-3.1-405B-Instructのデプロイ

量子化とは

大規模言語モデル（LLM）は、その名のとおり、とてもパラメーター数が多く、動作させるためには大量のGPUメモリーを消費します。　　
限りあるGPUメモリーで、なるべくパラメーター数の多い、性能の良いLLMを動作させたいという要求には、量子化というテクニックを用いるのが一般的です。量子化と言えば、物理学の世界では、アナログ信号などの連続値を、デジタル信号などの離散値へ変換することを指しますが、AIの世界では、デジタル信号の精度を、高精度なデータ形式から低精度なデータ形式へ変換することを指すのが一般的です。
　　
本記事は、後者の解釈に従って説明を続けます。たとえば、倍精度（64ビット）浮動小数点形式から、半精度（16ビット）浮動小数点形式へLLMのパラメーターを変換することにより、単純計算で、パラメーターが占有するGPUメモリー容量は1/4に削減されます。また、量子化により計算量削減やデータ転送時間短縮による推論時間の高速化も期待できます。

NVIDIA Blackwell世代GPUがサポートするデータ形式

では、最新のNVIDIA Blackwell世代GPUでは、どのようなデータ形式がサポートされているのでしょうか？以下に、Blackwell世代GPUとHopper世代GPUがサポートするデータ形式を示しました。ご覧のとおり、Blackwell世代GPUでは、6ビット浮動小数点（FP6）型と、4ビット浮動小数点（FP4）型が新たにサポートされました。本記事では、このFP4の利用方法について説明いたします。　　
出典:https://www.nvidia.com/ja-jp/data-center/tensor-cores/

	Blackwell	Hopper
Tensor コア精度	FP64, TF32, BF16, FP16, FP8, INT8, FP6, FP4	FP64, TF32, BF16, FP16, FP8, INT8
CUDA® コア精度	FP64, FP32, FP16, BF16	FP64, FP32, FP16, BF16, INT8

浮動小数点のデータ形式

FP4の話に進む前に、そもそも浮動小数点データはメモリー内でどのように表現されるのか見てみましょう。

FP32

AI分野に限らず、あらゆるアプリケーションで一般的に利用される単精度（32ビット）浮動小数点（FP32）を取り上げます。この形式は、IEEE754 binary32として規格化されております。下図をご覧ください。一般的に、浮動小数点は、符号ビット（S）、指数部、仮数部の3個の要素から構成されます。

符号ビットは、符号を表し、IEEE754では、0が正の値、1が負の値を表現します。仮数部は、正規化された2進数で表現されます。正規化とは、上位桁にゼロが出現しないように調整することで、以下がその例です。

\(1.001_2×2^5\)　（正規化数）

\(0.1001_2×2^6\)　（非正規化数）

仮数を\(M\)とすると、仮数部は以下のように符号化されています。\(i\)はビットインデックス、\(b_i\)はビット\(i\)の値です。\(1\)を足しているのは、正規化数の暗黙の\(1\)です。

\[ M=1+\sum_{i=0}^{22}b_{i}2^{i-23} \]

つまり、仮数部の各ビットは以下のような2進数を表現しています。

指数部の符号化は少し複雑です。それは、無限大、NaN（Not a Number）、非正規化数も表現するためです。以下のとおり、正規化数を示すのは、指数部が\(0000:0001_2\)～\(1111:1110_2\)に収まる範囲の場合です。

上記を総合すると、正規化数は以下の式で10進数に変換できます。\(M\)は前述のとおり仮数を、\(E\)は指数部の値です。

\[ (-1)^s\times{M}\times{2}^{E-127} \]

例を示してみましょう。IEEE754 binary32形式で、\(0011:1111:1110:0000:0000:0000:0000:0000_2\)を10進数に戻します。
符号ビット：\(0_2\)
指数部：\(0111:1111_2=127\)
仮数部：\(110:0000:0000:0000:0000:0000_2\)⇒\({1}\times{2}^{-1}+{1}\times{2}^{-2}=\dfrac{1}{2}+\dfrac{1}{4}=\dfrac{3}{4}=0.75\)
仮数部の値に暗黙の\(1\)を足して、\(M=1+0.75=1.75\)
上記から、以下のとおりです。

\[ (-1)^s\times{M}\times{2}^{E-127} ={-1}^{0}\times{1.75}\times{2}^{(127-127)} ={1}\times{1.75}\times{1} =1.75 \]

FP8

8ビット浮動小数点の場合は、指数部と仮数部のビット割り当てにより、2種類のバリエーションが存在します。　　
また、本記事の主題はFP4ですが、Blackwell世代のGPUではブロックスケーリングを組み合わせたMXFP8に対応しています。　　
これにより、既存のFP8演算と比較して精度が向上しています。詳細はFP4の章をご参照ください。

	E4M3	E5M2
指数バイアス	\(7\)	\(15\)
無限大	表現できない	\(S:11111:00_2\)
NaN	\(S:1111:111_2\)	\(S:11111:\{01, 10, 11\}_2\)
ゼロ	\(S:0000:000_2\)	\(S:00000:00_2\)
正規化数最大値	\(S:1111:110_2=\pm{2}^{8}\times{1.75}=\pm{448}\)	\(S:11110:11_2=\pm{2}^{15}\times{1.75}=\pm57344\)
正規化数最小値	\(S:0001:000_2=\pm{2}^{-6}\)	\(S:00001:00_2=\pm{2}^{-14}\)
非正規化数最大値	\(S:0000:111_2=\pm{2}^{-6}\times{0.875}\)	\(S:00000:11_2=\pm{2}^{-14}\times{0.75}\)
非正規化数最小値	\(S:0000:001_2=\pm{2}^{-9}\)	\(S:00000:01_2=\pm{2}^{-16}\)

FP4 E2M1

NVIDIA Blackwell世代GPUがサポートする4ビット浮動小数点形式（FP4）は、以下のとおり符号部1ビット、指数部2ビット、仮数部1ビットで構成（E2M1）されます。

仮数部で表現できる値は以下の2通りです。正規化数なので、暗黙の1が足されることに注意してください。

\(1+0\times{2}^{-1}=1.0\)
\(1+1\times{2}^{-1}=1.5\)

指数部で表現できる指数値は、バイアスが\(1\)と規定されているので、以下の3通りになります。なお、指数部が\(00_2\)のときは、特別な意味を持ちます。

\(1-1=0\)
\(2-1=1\)
\(3-1=2\)

ゼロは\(S:00:0_2\)で表現されます。\(S\)は符号ビットです。
無限大およびNaN（Not a Number）は表現できません。
\(S:00:1_2\)は非正規化数とされ、\(\pm{0.5}\)を表します。
以上を総合すると、FP4 E2M1が表現できる値は以下のようになります。

ビット3	ビット2	ビット1	ビット0	値
0	0	0	0	0
0	0	0	1	0.5
0	0	1	0	1
0	0	1	1	1.5
0	1	0	0	2
0	1	0	1	3
0	1	1	0	4
0	1	1	1	6
1	0	0	0	-0
1	0	0	1	-0.5
1	0	1	0	-1
1	0	1	1	-1.5
1	1	0	0	-2
1	1	0	1	-3
1	1	1	0	-4
1	1	1	1	-6

スケーリング

上記のとおり、FP4 E2M1形式は、\(-6\)～\(+6\)の範囲しか表現できません。しかし、推論中のLLMの中では、もっと広い範囲の数値が存在します。そのため、スケーリングという仕組みで実際の値を表現します。例えば、スケーリング係数を\(100\)と仮定すれば、\(-600\)～\(+600\)を表現できます。
但し、このような単純なスケーリングでは、精度は依然、とても低いままです。ここで、ブロック毎にスケーリング係数を変える工夫が登場します。この工夫には、単純ではありますが、大量の計算が発生するので、NVIDIA Blackwell世代GPUでは、スケーリングをハードウェアで高速化します。
一つ一つの数値は、FP4 E2M1という形式で符号化されますが、スケーリングのブロックサイズや、スケーリング係数の形式まで規定する必要が生じて来ると、それらを全部ひっくるめた形式に対する名称が必要になります。以下に、まずは、MXFP4と呼ばれる形式を紹介し、最後に本記事の主題であるNVFP4をご紹介いたします。

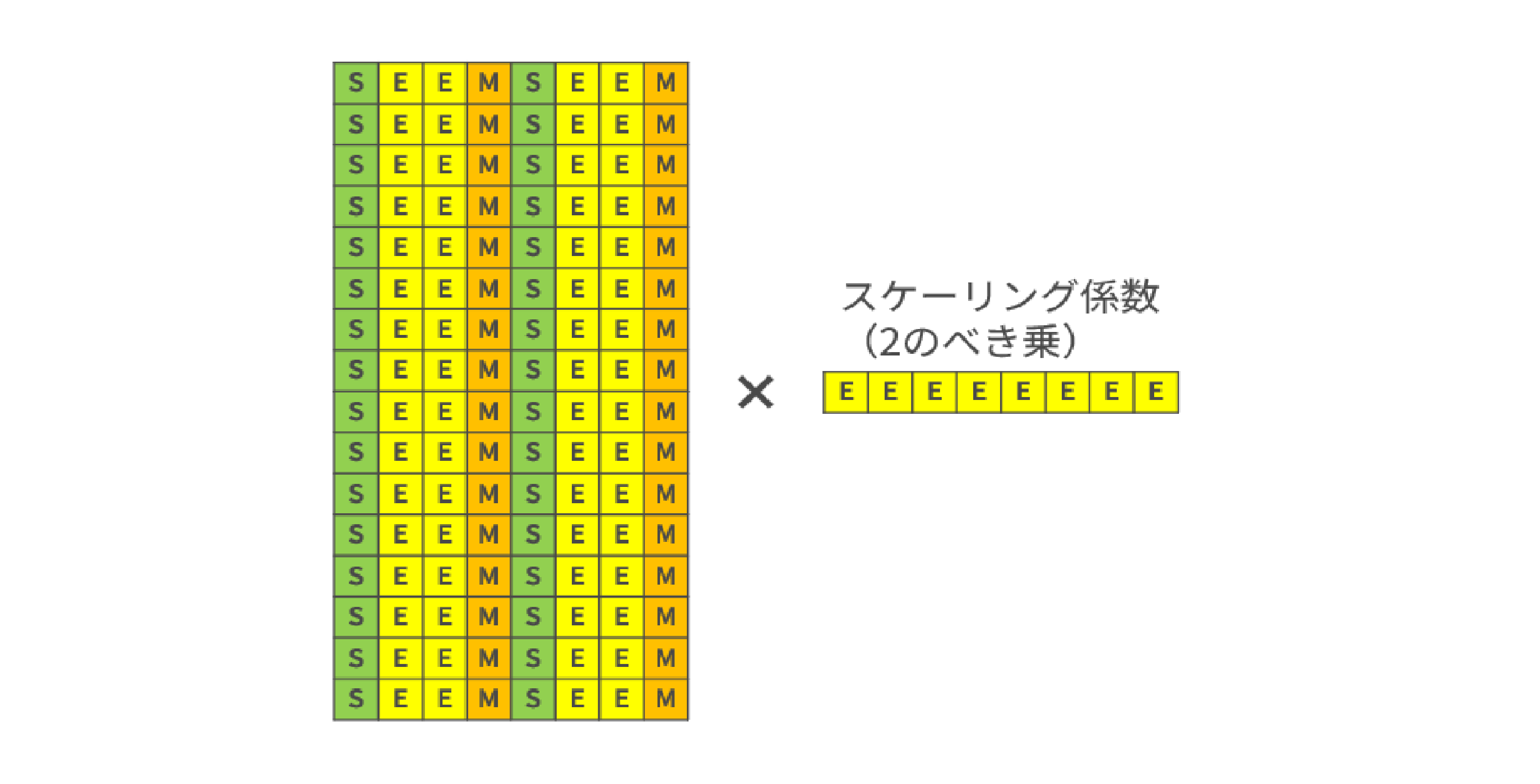
MXFP4

まずは、MXFP4と呼ばれる形式をご紹介します。この形式は、32個のFP4 E2M1値毎に、1個のE8M0スケーリング係数を共有します。
E8M0はスケーリング係数専用のデータ形式で、全8ビットが指数を表現します。バイアスは\(127\)で、表現できる指数の範囲は、\(-127\)～\(+127\)です。よって、スケーリング係数は必ず2のべき乗になります。

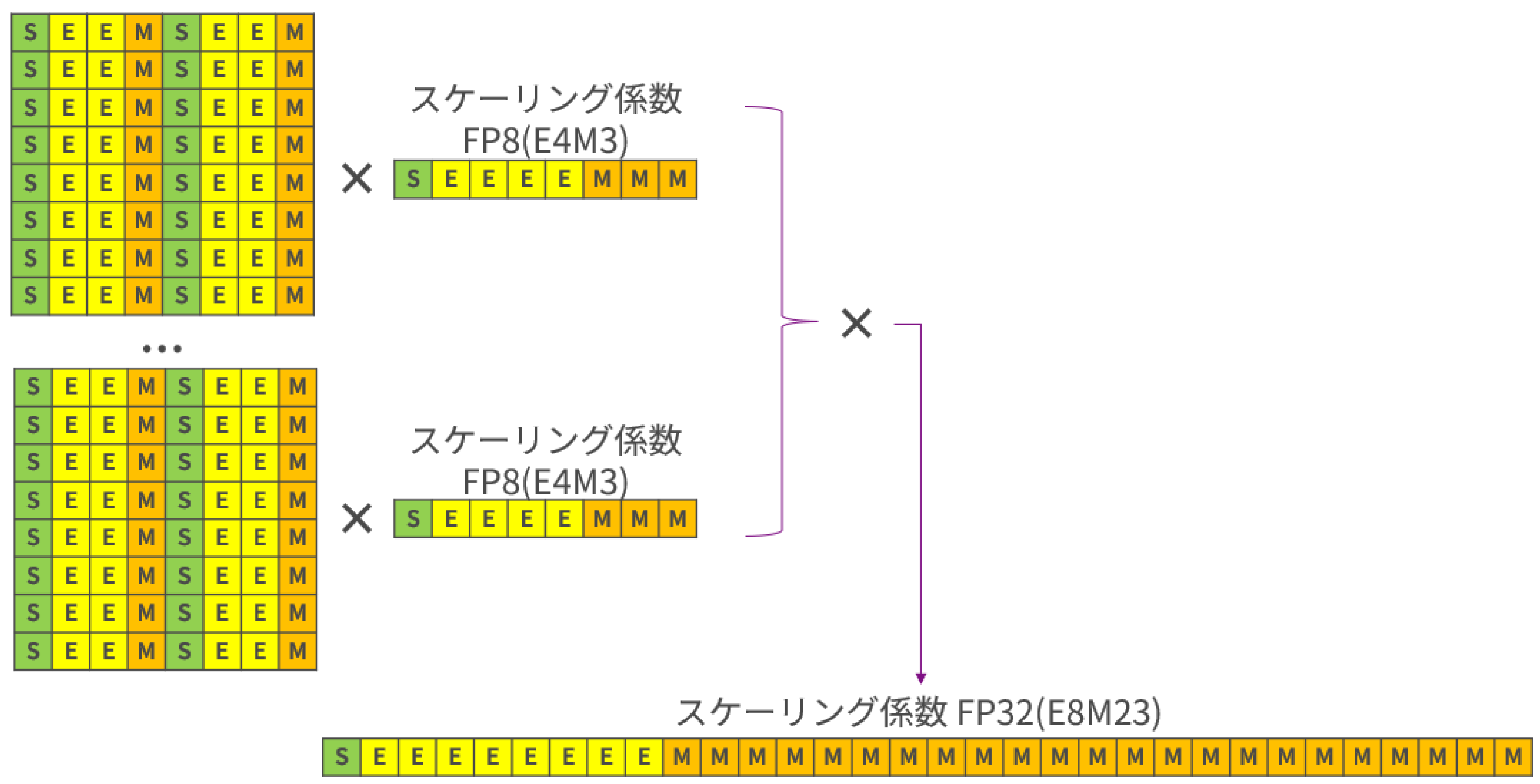
NVFP4

最後に、本記事の主題であるNVFP4をご紹介いたします。この形式は、16個のFP4 E2M1値毎に1個のFP8(E8M0)スケーリング係数を共有します。MXFP4よりも細かなブロック、かつ、スケーリング係数を浮動小数点型にすることで、高い精度を実現します。但し、そうすることで表現できる数値の範囲がMXFP4よりも狭くなってしまうので、2段目のスケーリング係数をテンサー単位で設定します。2段目のスケーリング係数は、本記事の最初でご紹介したFP32です。

まとめ

NVIDIA Blackwell世代GPUで、新しくサポートされた4ビット浮動小数点型NVFP4についてご紹介いたしました。4ビットという大胆なビット削減にも関わらず、16値ブロックあたりの細かなスケーリング、8ビット浮動小数点型のスケーリング係数、2段目の32ビット浮動小数点スケーリング係数により、精度を損なわずにLLM推論が実現できます。

特徴	テンサー単位のスケーリングによるFP4 (E2M1)	MXFP4	NVFP4
フォーマット構造	4ビット(1符号、2指数、1仮数)とソフトウェアスケーリングファクター	4 ビット (1 符号、2 指数、1 仮数) と 32 値ブロックあたり 1 つの共有 2 の累乗スケール	4 ビット (1 符号、2 指数、1 仮数) と 16 値ブロックあたり 1 つの共有 FP8 スケール
ハードウェアによるスケーリングの高速化	いいえ	はい	はい
メモリー要求	FP16の~25%	FP16の~25%	FP16の~25%
精度	FP8と比較して精度が著しく低下するリスク	FP8と比較して精度が著しく低下するリスク	特に大型モデルの場合、顕著な精度低下は起こりづらい