浮動小数点の構造

小数の位置を固定せずに表現するため、表し方は 10 進数の指数の表現のようになります。

以下のように表します。

同じようにこの「符号」、「仮数」、「指数」ビットで表現します。浮動小数点では 32 ビットを以下のように 3 つに分割します。

では、この図に数字を入れながら、それぞれがどのように表されるかを見ていきましょう。

例として、－10.25 をビットで表現してみます。

仮数部の表し方

仮数部は実際の数字を表す部分になります。 2 進数の場合、整数では桁が上がるにつれ 2 の乗数を表していましたが、 小数では桁が下がるにつれ 0.5 の乗数 ( 2 のマイナス乗) を表します。

2 のマイナス乗ずつ加算していくので、ぴったり表せないこともあります。その場合は近い値で近似してあらわすことになります。

－10.25 の場合を見てみましょう。まずは小数点以下の 0.25 の部分はどう表現するのでしょうか？

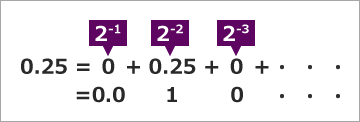
仮数部はこの小数部分と整数部分を合わせた数になります。整数部分は 10 なので簡単に 2 進数に変換できますね。これらを合わせた変換の方法は以下の図のようになります。

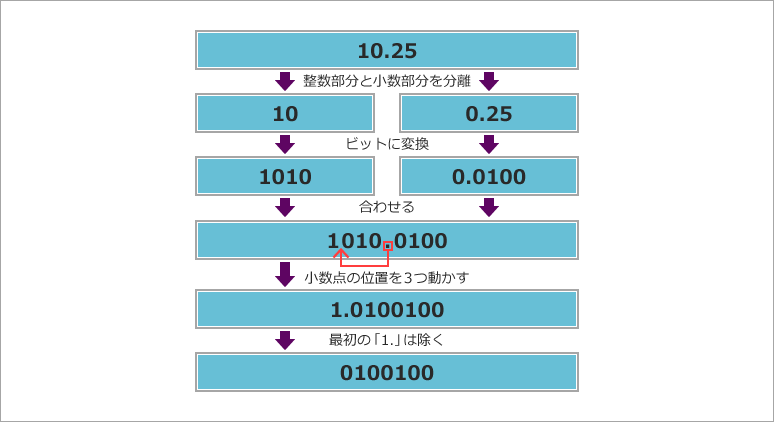
整数部分と小数部分をそれぞれビットに変換し、それを合わせます。その後、整数部分が “1” で一桁になるように小数点を移動します。

そうするとビットとしては整数部分が常に 1 になります。そのため、最初の 1 を除いた 0100100… が仮数部の数字となります。残りの桁には 0 が入ります。

一番ビット数の多いところが埋まると、ついにゴールが見えてきましたね。ここまで来ると後少しです。

指数部の求め方

指数部は 10 進数の時と同じく、動かした小数点の数を表します。仮数部を求めるときに動かしたのが 3 桁なので指数部は 3 となります。

そこで指数部を 0000 0011 としたいところですが、そうは問屋が卸してくれません。この指数部はオフセットバイナリ形式で数を表します。バイアス値 127 となります。

そのため、以下の図のようにバイアス値 127 を足して 1000　0010 が指数部となります。

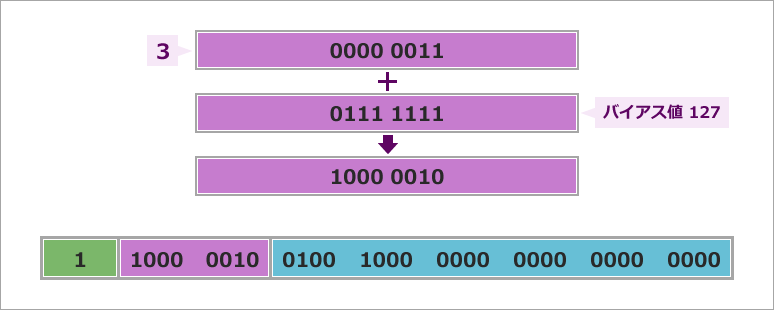
これで －10.25 を浮動小数点で表すことができました。

補足ですが、仮数部の説明で最上位を 1 にするといいました。しかし、一つだけ例外があります。それは 0 の時です。そのため例外的に 0 の時は浮動小数点でもすべてのビットが 0 になります。

覚えておきたい＋α

今回の内容で、正の数・負の数・小数・指数も表すことができました。ただ、浮動小数点を使った演算は、各数値の小数点位置を合わせたり、オーバーフローをチェックしたりと複雑です。そのため専用の演算処理装置を組み込むことが多いです。

そして、インテル®  FPGA ではデジタル演算処理 ( DSP ) ブロックが組み込まれており、浮動小数点演算を実施することが可能です。また Arria® V SoC、Cyclone® V SoC 以降の SoC デバイスや FPGA では浮動小数点演算がハードウェア実装されています。