The Laplace and Fourier transforms have been previously mentioned below.

Laplace transform and Fourier transform
Laplace transform and Fourier transform Part 2

In "Laplace Transform and Fourier Transform Part 2", we used a polygonal line as the signal source.
As a result, the FFT cannot faithfully reproduce the high-frequency component of the bend, so it is necessary to compare the waveforms with smooth waveforms, as I mentioned earlier.

As a smooth signal source, we use a waveform obtained by passing a rectangular waveform through a Bessel filter.
See below for Bessel filters.

Difference between Bessel filter and other filters Part 1
Difference between Bessel filter and other filters Part 2

As I said before, the Laplace transform is a transient phenomenon and the Fourier transform is a periodic function, so we need to use the following two methods to make a rigorous comparison.

(1) Approximating the Fourier transform to a solitary wave
(2) Quasi-periodize the Laplace transform

For (1), choose a small signal duty ratio. Even if the same pulse width is analyzed, if the duty ratio is halved (the period is doubled), the effective N of the Fourier transform will be halved. You will need.

(2) is explained in Fig. 1.

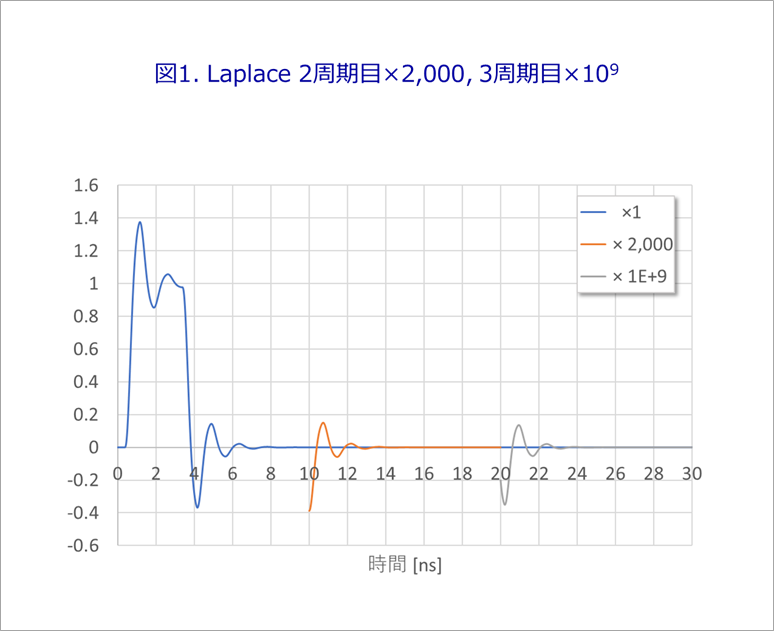
Here, the period T of the Fourier transforms to be compared is set to 10ns.
The blue line in Fig. 1 is a Laplace-transformed single reflection waveform with a pulse width of 3 ns.
In the figure, the oscillation (reflection) of the waveform seems to settle down after a few ns, but if you magnify the area around 10 ns by 2,000 times (orange line), you can see the remnants of the reflection.
Furthermore, if we zoom in around 20ns to the 9th power of 10 (gray line), the reflection is still not completely settled.
Therefore, to pseudo-periodize the Laplace transform, we need to add the remnants of reflections after 10 ns and after 20 ns in Fig. 1 to the original pulse waveform.

Note that (1) and (2) are methods used to strictly compare the Laplace transform and the Fourier transform, and are not necessary in practice.

Figure 2(a) shows the difference between the single-shot waveform and the inverse Fourier transform.
The blue line is the difference (left axis scale) with a maximum error of about 200ppm. The gray line (right axis scale) is the signal.

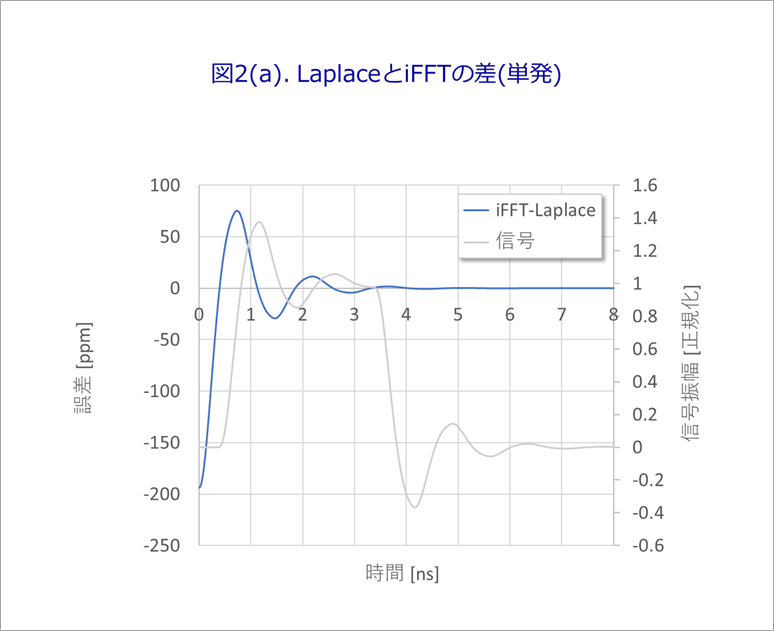
The reason for this is the overlap of the orange waveform near 10ns and the gray waveform near 20ns in Figure 1.

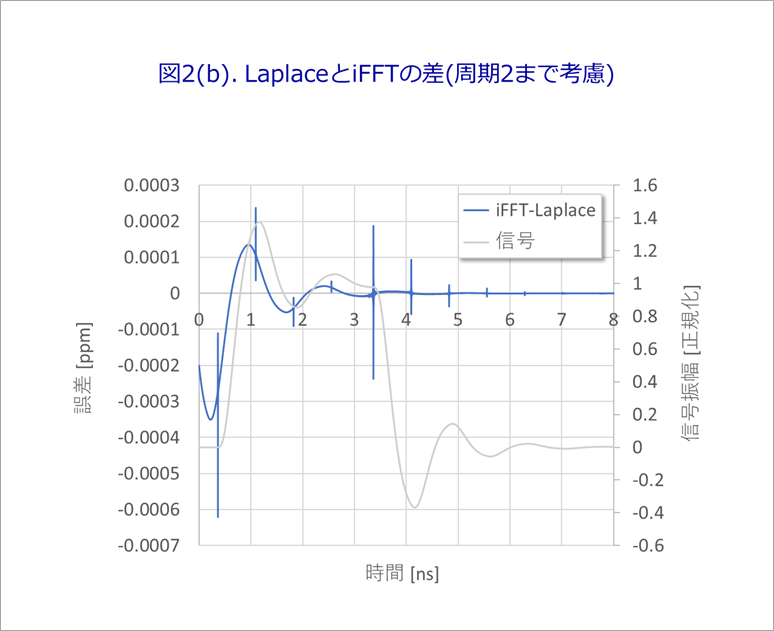
Fig. 2(b) is a Laplace transform superimposed with an orange waveform and compared with the Fourier transform.
The maximum error was 0.0006ppm at the peak, almost zero.

Furthermore, when the gray waveform in Fig. 1 is superimposed, only needle-like errors are obtained, as shown in Fig. 2(c).

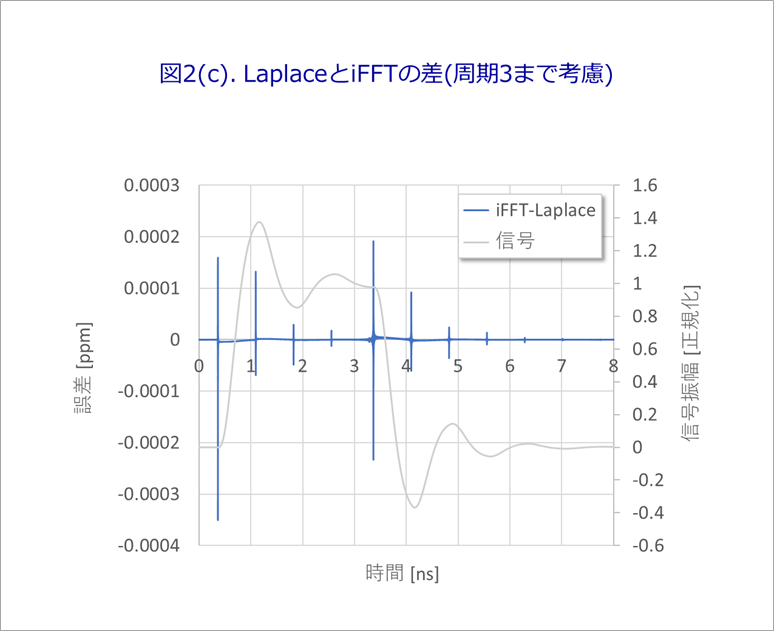
Figure 3 shows the signal waveform overlaid on Figure 4 of "Laplace Transform and Fourier Transform 2".

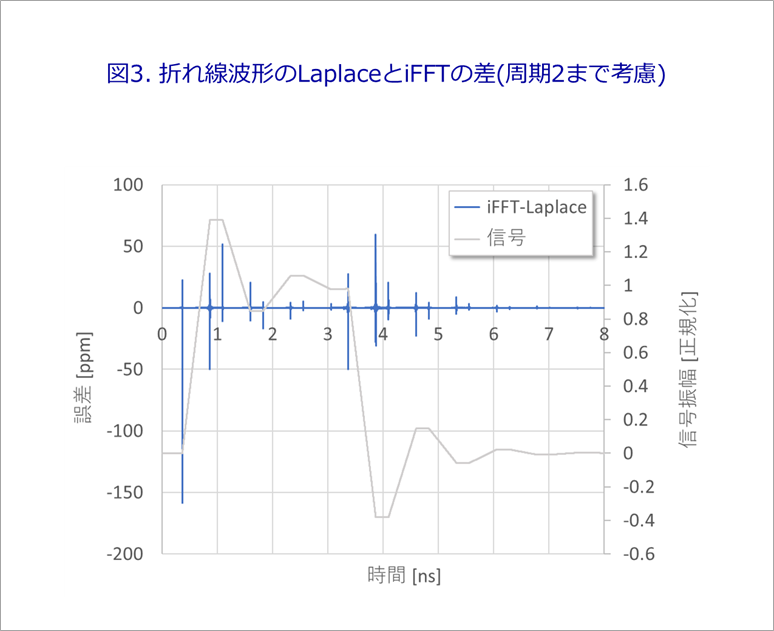
In the case of a broken line signal, the error becomes large at the time of change, and the maximum error is about 150ppm.
Comparing Fig. 2(c) and Fig. 3, there is a difference of more than five orders of magnitude.

In the figures above, the iFFT N is 16,384.

Next, we will verify the iFFT N and analysis error.

First is the error in the case of the line signal.

Figure 4 shows the error for iFFT N=256 and N=512. 3,000ppm to 4,000ppm, or 0.3% to 0.4% error.

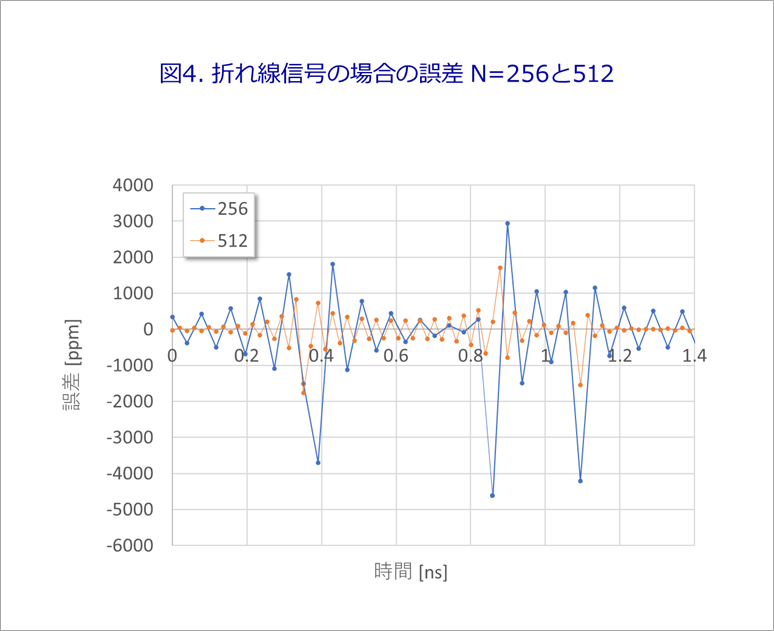
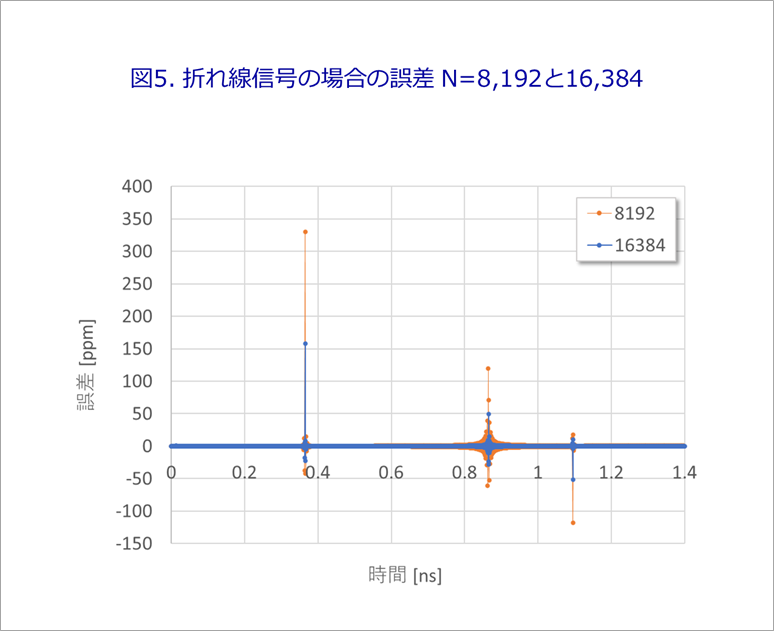
Figure 5 shows the error for N=8,192 and N=16,384. The plateaus are small errors, but as mentioned earlier, the corners of the waveform introduce errors.

To verify the error, calculate the standard error = Root Mean Square (RMS) of the timing error at each time.

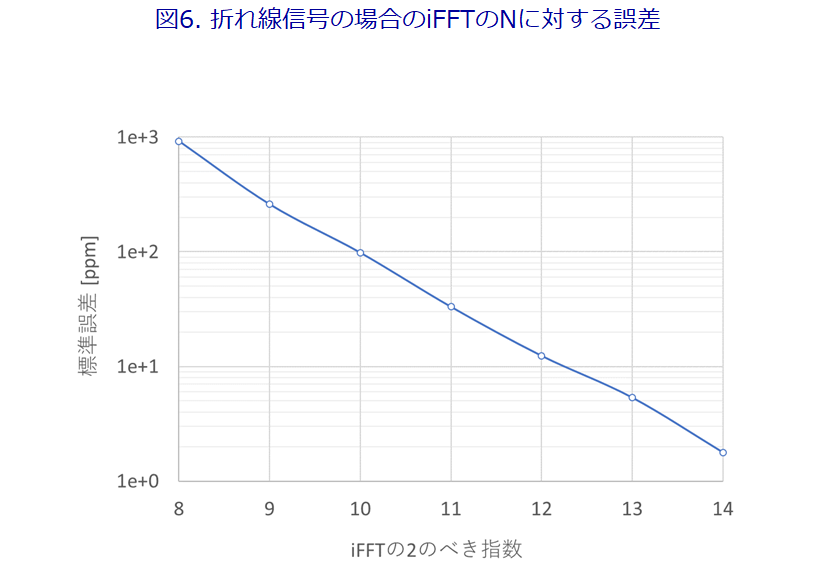
Figure 6 shows the iFFT error versus N for the line signal. The horizontal axis is the exponent of 2 in the FFT, for example, if the horizontal axis is 10, N is 2 to the 10th power, or 1,024.
N=16,384 (2 to the 14th power), and the standard error is about 2ppm.

Next, we verify the case of a smooth signal using the Bessel LPF.

Figure 7 shows the errors for the Bessel LPF for N=256 and 512. Compare with Figure 4 of the line.
In the case of N=256, the peak error is about 60ppm, and in the case of N=512, even the peak is less than 10ppm.

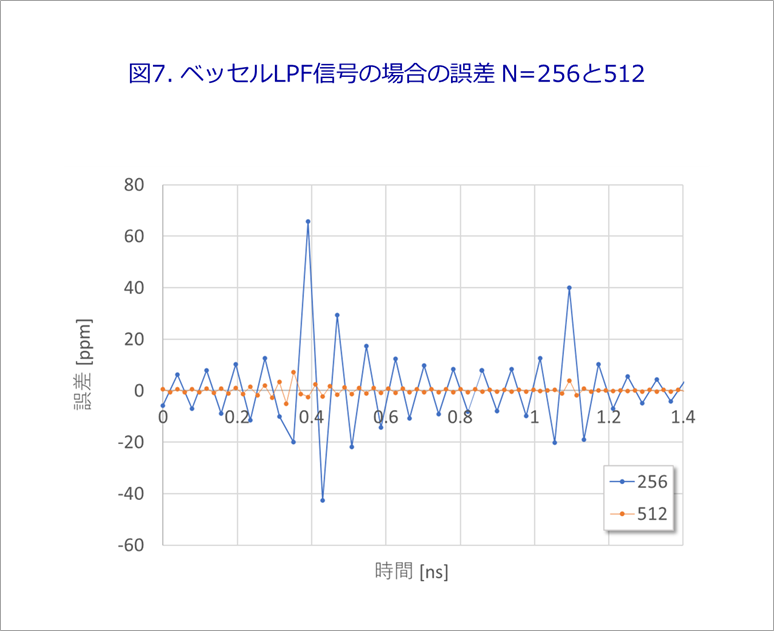
Figure 8 shows the errors for the Bessel LPF for N=8,192 and 16,384. Compare with Figure 5 of the line.
In either case, the error is extremely small.

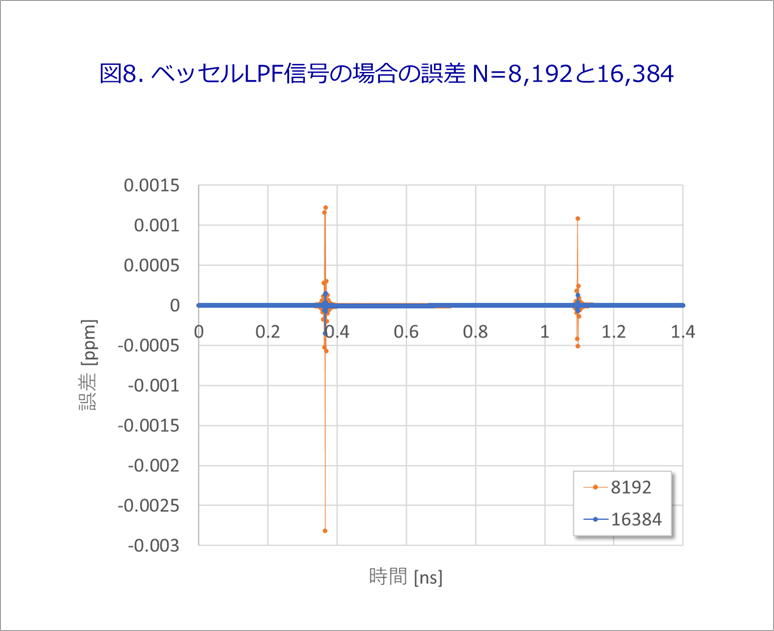
Figure 9 is the standard error for the Bessel LPF, corresponding to Figure 6 of the line.
N=256 (2 to the power of 8) is about 10ppm.
The error decreases by more than one order of magnitude corresponding to increasing powers of 2.

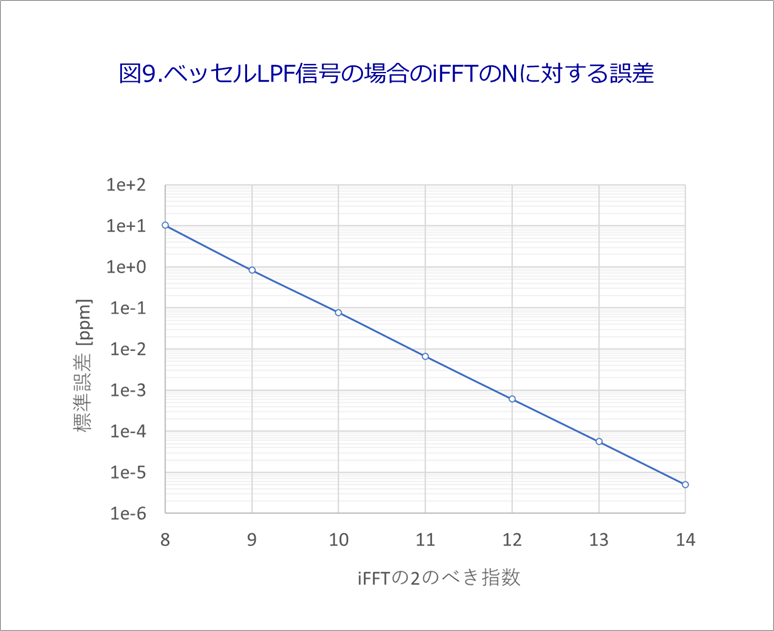
Practically, even N=256 is considered to be sufficient accuracy (error).

Figure 10 is a comparison of iFFT (N=256) and Laplace waveforms for the polygonal line.
The iFFT shows a zigzag undulation in the plateau after the first rise.

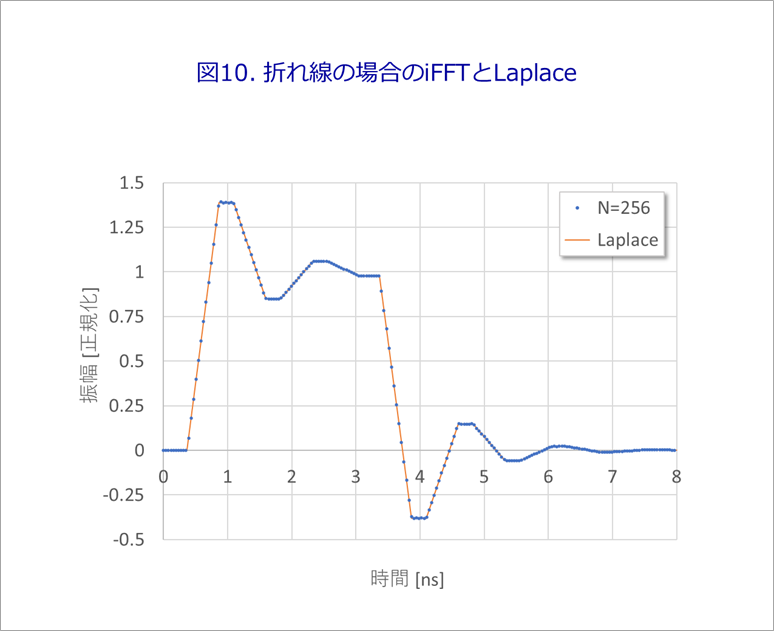
The error between the two is the Prue waveform in Figure 7.
There is an error of about 60ppm around 0.4ns.

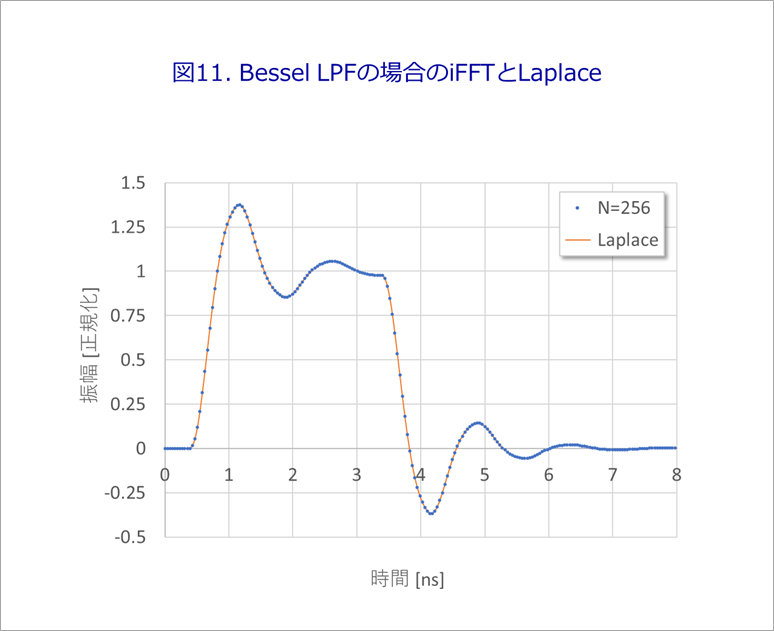
Figure 11 compares the iFFT (N=256) and Laplace waveforms when a square wave is passed through a Bessel LPF.
As far as I can see, there is no discrepancy (error) between the two waveforms.

How to choose N for the Fourier transform depends on the high-frequency component of the waveform to be analyzed, but in the case of a normal reflected waveform, if it is a polygonal line waveform, it should be 1,024.
In this case, the standard error is around 100ppm. See Figure 6.

In the case of waveforms generated by the Bessel LPF instead of the line, according to Fig. 9, even with N=256, the standard error is 10ppm, so I think it is sufficient.

Fourier transforms and Bessel LPFs have been discussed in several parts.
Fortunately, the performance of PCs has improved, and even high-order iFFTs with N = 4,096 do not seem to have any performance problems.
I hope you will take advantage of it.
In my environment (Core i5-12600KF), I felt that N=16,384 was the limit.